(本小题满分14分)设椭圆
 的左焦点为
的左焦点为 ,上顶点为
,上顶点为 ,过点
,过点 与
与 垂直的直线分别交椭圆
垂直的直线分别交椭圆 与
与 轴正半轴于点
轴正半轴于点 ,且
,且 . ⑴求椭圆
. ⑴求椭圆 的离心率;⑵若过
的离心率;⑵若过 、
、 、
、 三点的圆恰好与直线
三点的圆恰好与直线
 相切,求椭圆
相切,求椭圆 的方程.
的方程. 
已知椭圆的中心为原点 ,长轴在 轴上,上顶点为 ,左、右焦点分别为 ,线段 的中点分别为 ,且 是面积为4的直角三角形.
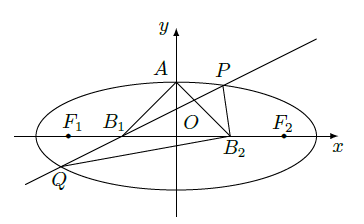
(Ⅰ)求该椭圆的离心率和标准方程;
(Ⅱ)过
作直线交椭圆于
,
,求
的面积.
已知直三棱柱 中, , 为 的中点.
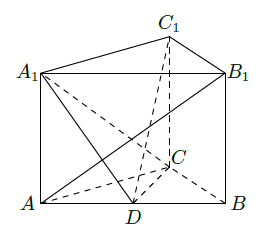
(Ⅰ)求异面直线
和
的距离;
(Ⅱ)若
,求二面角
的平面角的余弦值.
设函数 (其中 )在 处取得最大值2,其图象与轴的相邻两个交点的距离为 .
(I)求 的解析式;
(II)求函数 的值域.
甲、乙两人轮流投篮,每人每次投一球,约定甲先投且先投中者获胜,一直每人都已投球3次时投篮结束,设甲每次投篮投中的概率为 ,乙每次投篮投中的概率为 ,且各次投篮互不影响.
(Ⅰ)求乙获胜的概率;
(Ⅱ)求投篮结束时乙只投了2个球的概率.
已知函数 在 处取得极值为
(1)求
的值;
(2)若
有极大值28,求
在
上的最大值.