8分)
已知集合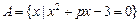 ,集合
,集合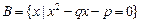 ,且
,且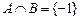 ,求
,求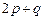 的值.
的值.
(本小题满分10分)选修4—1:几何证明选讲
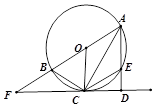
如图,已知 是
是 的直径,
的直径,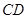 是
是 的切线,
的切线, 为切点,
为切点,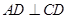 ,交
,交 于点
于点 ,连接
,连接 、
、 、
、 、
、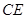 ,延长
,延长 交
交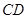 于
于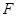 .
.
(1)证明: ;
;
(2)证明: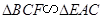 .
.
(本小题满分14分)设函数 (
( ).
).
(1)当 时,求
时,求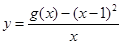 的极值;
的极值;
(2)求函数 的单调递增区间;
的单调递增区间;
(3)若函数 有两个极值点
有两个极值点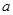 ,
, ,且
,且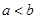 ,记
,记 表示不大于
表示不大于 的最大整数,试比较
的最大整数,试比较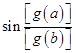 与
与 的大小.
的大小.
(本小题满分12分)数列 的前n项和为
的前n项和为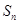 ,且
,且
(1)求数列 的通项公式;
的通项公式;
(2)若数列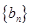 满足:
满足: ,求数列
,求数列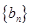 的通项公式;
的通项公式;
(3)令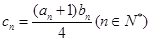 ,求数列
,求数列 的 n项和
的 n项和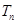 .
.
(本小题满分14分)为了保护环境,某工厂在国家的号召下,把废弃物回收转化为某种产品,经测算,处理成本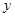 (万元)与处理量
(万元)与处理量 (吨)之间的函数关系可近似的表示为:
(吨)之间的函数关系可近似的表示为: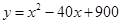 ,
,
(1)当处理量为多少吨时,每吨的平均处理成本最少?
(2)若每处理一吨废弃物可得价值为 万元的某种产品,同时获得国家补贴
万元的某种产品,同时获得国家补贴 万元.当
万元.当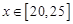 时,判断该项举措能否获利?如果能获利,求出最大利润;如果不能获利,请求出国家最少补贴多少万元,该工厂才不会亏损?
时,判断该项举措能否获利?如果能获利,求出最大利润;如果不能获利,请求出国家最少补贴多少万元,该工厂才不会亏损?
(本小题满分13分)已知椭圆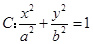
 的离心率为
的离心率为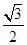 ,直线
,直线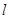 经过椭圆的上顶点
经过椭圆的上顶点 和右顶点
和右顶点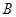 ,并且和圆
,并且和圆 相切.
相切.
(Ⅰ)求椭圆 的方程;
的方程;
(Ⅱ)设直线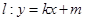 (
( )与椭圆
)与椭圆 相交于
相交于 、
、 两点,以线段
两点,以线段 、
、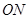 为邻边作平行四边形
为邻边作平行四边形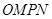 ,其中顶点
,其中顶点 在椭圆
在椭圆 上,(其中
上,(其中 为坐标原点),求
为坐标原点),求 的取值范围.
的取值范围.