杨辉是中国南宋末年的一位杰出的数学家、数学教育家,杨辉三角是杨辉的一大重要研究成果,它的许多性质与组合数的性质有关,杨辉三角中蕴藏了许多优美的规律.下图是一个11阶杨辉三角:
(1)求第20行中从左到右的第3个数;
(2)若第 行中从左到右第13与第14个数的比为
行中从左到右第13与第14个数的比为 ,求
,求 的值;
的值;
(3)写出第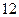 行所有数的和,写出
行所有数的和,写出 阶(包括
阶(包括 阶)杨辉三角中的所有数的和;
阶)杨辉三角中的所有数的和;
(4)在第3斜列中,前5个数依次为1,3,6,10,15;第4斜列中,第5个数为35,我们发现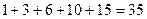 ,事实上,一般地有这样的结论:第
,事实上,一般地有这样的结论:第 斜列中(从右上到左下)前
斜列中(从右上到左下)前 个数之和,一定等于第
个数之和,一定等于第 斜列中第
斜列中第 个数.
个数.
试用含有 ,
,
 的数学式子表示上述结论,并证明.
的数学式子表示上述结论,并证明.
(本小题满分14分)已知集合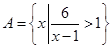 ,
,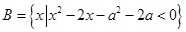 .
.
(1)当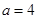 时,求
时,求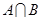 ;
;
(2)若 ,求实数
,求实数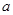 的取值范围.
的取值范围.
(本小题满分14分)(1)已知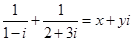 ,求实数
,求实数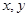 的值;
的值;
(2)已知 ,若
,若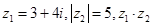 是纯虚数,求
是纯虚数,求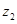
(本小题满分14分)已知命题p:方程x2+mx+1=0有两个不相等的实根;q:不等式4x2+4(m–2)x+1>0的解集为R.
(1)若命题q为真,求实数m的取值范围.
(2)若命题“p且q”和“非p”为假,求实数m的取值范围
设正项数列{an}(n≥5)对任意正整数k(k≥3)恒满足: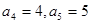 ,且
,且 .
.
(1)求数列{an}的通项公式;
(2)是否存在整数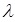 ,使得
,使得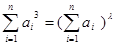 对于任意正整数n恒成立?若存在,求出
对于任意正整数n恒成立?若存在,求出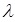 的值;若不存在,说明理由。(注:
的值;若不存在,说明理由。(注: )
)
一个正方形花圃,被分为n( )份,种植红、黄、蓝、绿4种颜色不同的花,要求相邻两部分种植不同颜色的花。
)份,种植红、黄、蓝、绿4种颜色不同的花,要求相邻两部分种植不同颜色的花。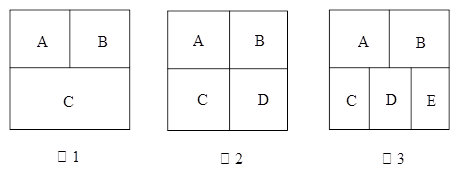
(1)如图1,正方形被分为3份A、B、C,有多少种不同的种植方法?
(2)如图2,正方形被分为4份A、B、C、D,有多少种不同的种植方法?
(3)如图3,正方形被分为5份A、B、C、D、E,有多少种不同的种植方法?