(本小题满分12分)
某校举办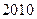 年上海世博会知识竞赛,从参赛的高一、高二学生中各抽
年上海世博会知识竞赛,从参赛的高一、高二学生中各抽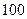 人的成绩作
人的成绩作
 |
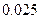 |
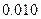 |
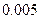 |
 |
 |
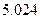 |
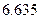 |
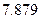 |
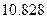 |
为样本,其结果如下表:
参考数据:
| |
高一 |
高二 |
合计 |
| 合格人数 |
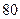 |
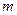 |
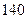 |
| 不合格人数 |
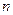 |
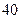 |
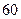 |
| 合计 |
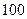 |
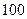 |
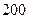 |
(Ⅰ)求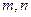 的值;
的值;
(Ⅱ)你有多大的把握认为“高一、高二两个年级这次世博会知识竞赛的成绩有差异”.
已知数列 满足
满足 ,
,
 .
.
(1)令 ,求证:数列
,求证:数列 为等比数列;
为等比数列;
(2)求满足 的最小正整数
的最小正整数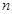
设条件p:|x-2|<3,条件q:0<x<a,其中a为正常数.若p是q的必要不充分条件,则a的取值范围是()
A. |
B. |
C. |
D. |
函数
(1)当 时,求函数
时,求函数 在[-1,3]的最值
在[-1,3]的最值
(2)当 ,
, 恒成立,求实数
恒成立,求实数 的取值范围.
的取值范围.
据气象中心观察和预测:发生于M地的沙尘暴一直向正南方向移动,其移动速度v(km/h)与时间t(h)的函数图象如图所示,过线段OC上一点T(t,0)作横轴的垂线 ,梯形OABC在直线
,梯形OABC在直线 左侧部分的面积即为t(h)内沙尘暴所经过的路程s(km).
左侧部分的面积即为t(h)内沙尘暴所经过的路程s(km).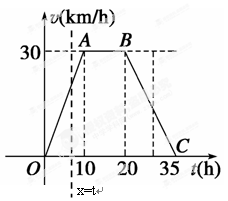
(1)当t=4时,求s的值;
(2)将s随t变化的规律用数学关系式表示出来;
(3)若N城位于M地正南方向,且距M地650 km,试判断这场沙尘暴是否会侵袭到N城,如果会,在沙尘暴发生后多长时间它将侵袭到N城?如果不会,请说明理由.
已知函数 是奇函数
是奇函数
(1)求实数 的值;
的值;
(2)判断并证明函数单调性.