（本小题满分13分）
甲乙两名射手互不影响地进行射击训练，根据以往的数据统计，他们设计成绩的分布列如下：
| 射手甲 |
射手乙 |
||||||
| 环数 |
8 |
9 |
10 |
环数 |
8 |
9 |
10 |
| 概率 |
 |
|
|
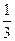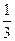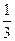概率 |
|
 |
 |
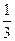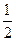（1）若甲射手共有5发子弹，一旦命中10环就停止射击，求他剩余3颗子弹的概率；
（2）若甲乙两射手各射击两次，求四次射击中恰有三次命中10环的概率；
（3）若两个射手各射击1次，记所得的环数之和为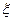
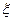，求的分布列和期望。
已知抛物线C的方程为
，A，B是抛物线C上的两点，直线AB过点M
。（Ⅰ）设
是抛物线上任意一点，求
的最小值；（Ⅱ）求向量
与向量
的夹角（O是坐标原点）；（Ⅲ）在
轴上是否存在异于M的一点N，直线AN与抛物线的另一个交点为D，而直线DB与轴交于点E，且有
？若存在，求出N点坐标；若不存在，说明理由．
（本小题满分13分）
设不等式组
确定的平面区域为U，
确定的平面区域为V．（Ⅰ）定义坐标为整数的点为“整点”．
在区域U内任取3个整点，
求这些整点中恰有2个整点在区域V的概率；
（Ⅱ）在区域U内任取3个点，记此3个点在区域V的个数为X，
求X的概率分布列及其数学期望．
（本小题满分13分）
如图，在三棱锥
中，侧面
与侧面
均为等边三角形，
，
为
中点．
（Ⅰ）证明：
平面
；
（Ⅱ）求二面角
的余弦值．
设函数
，
，（Ⅰ）如果函数
的图像是由函数的图像上各点的横坐标伸长为原来的2倍，再把所得图像向左平移
得到，求函数
解析式；
（Ⅱ）如果
，求在区间
上的值域．
已知函数
．
（1）若函数在区间
（其中
）上存在极值，求实数a的取值范围；
（2）如果当
时，不等式
恒成立，求实数k的取值范围．