设数列 ,
,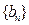 满足
满足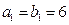 ,
,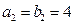 ,
, 。
。
(1)若 是等差数列,求
是等差数列,求 的通项公式;
的通项公式;
(2)若 是等比数列,求
是等比数列,求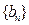 的通项公式;
的通项公式;
(3)在(1)、(2)的条件下,当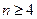 时,
时, 与
与 哪一个较大?证明你的结论。
哪一个较大?证明你的结论。
一种产品的产量原来是 ,在今后
,在今后 年内,计划使产量平均每年比上一年增加
年内,计划使产量平均每年比上一年增加 ,写出产量随年数变化的函数解析式.
,写出产量随年数变化的函数解析式.
某电器公司生产 型电脑.1993年这种电脑每台平均生产成本为5000元,并以纯利润
型电脑.1993年这种电脑每台平均生产成本为5000元,并以纯利润 确定出厂价.从1994年开始,公司通过更新设备和加强管理,使生产成本逐年降低.到1997年,尽管
确定出厂价.从1994年开始,公司通过更新设备和加强管理,使生产成本逐年降低.到1997年,尽管 型电脑出厂价仅是1993年出厂价的
型电脑出厂价仅是1993年出厂价的 ,但却实现了
,但却实现了 纯利润的高效益.
纯利润的高效益.
(1)求1997年每台 型电脑的生产成本;
型电脑的生产成本;
(2)以1993年的生产成本为基数,求1993年至1997年生产成本平均每年降低的百分数
(精确到 ,以下数据可供参考:
,以下数据可供参考: ,
, ).
).
已知函数 ,
, ,
, ,且
,且 .
.
(1)求函数 的定义域;
的定义域;
(2)判断函数 的奇偶性,并说明理由;
的奇偶性,并说明理由;
(3)求使 成立的
成立的 的集合.
的集合.
函数 ,
, ,
, 的图象如图所示.
的图象如图所示.
(1)试说明哪个函数对应于哪个图象,并解释为什么.
(2)以已有图象为基础,在同一坐标系中画出 ,
, ,
, 的图象.
的图象.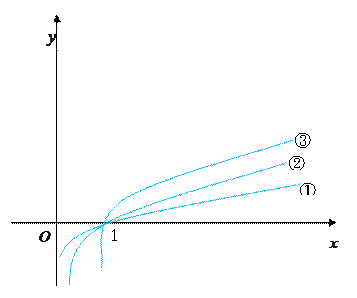
已知幂函数 的图象过点
的图象过点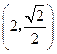 ,试求出此函数的解析式,
,试求出此函数的解析式,
并作出图象,判断奇偶性、单调性.