若矩阵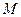 有特征向量
有特征向量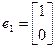 ,
,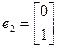 且它们所对应的一个特征值为
且它们所对应的一个特征值为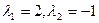
(1)求矩阵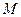 及其逆矩阵
及其逆矩阵 ;
;
(2)求 的特征值及特征向量;
的特征值及特征向量;
(3)对任意的向量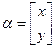 ,求
,求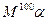 。
。
(本小题满分10分)
已知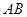 为半圆
为半圆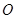 的直径,
的直径, ,
,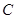 为半圆上一点,过点
为半圆上一点,过点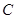 作半圆的切线
作半圆的切线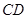 ,过点
,过点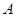 作
作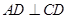 于
于 交圆于点
交圆于点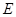 ,
,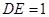 .
.
(1)求证: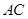 平分
平分 ;
;
(2)求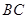 的长.
的长.
(本小题满分14分)
在平面直角坐标系中,已知向量 (
(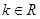 ),
),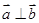 ,动点
,动点 的轨迹为
的轨迹为 .
.
(1)求轨迹 的方程,并说明该方程表示的曲线的形状;
的方程,并说明该方程表示的曲线的形状;
(2)当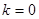 时,过点
时,过点 (0,1),作轨迹T的两条互相垂直的弦
(0,1),作轨迹T的两条互相垂直的弦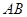 、
、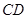 ,设
,设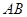 、
、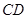 的中点分别为
的中点分别为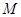 、
、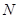 ,试判断直线
,试判断直线 是否过定点?并说明理由.
是否过定点?并说明理由.
(本小题满分14分)设数列 的前
的前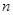 项和为
项和为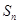 ,点
,点 在直线
在直线 上,
上, 为常数,
为常数,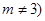 .
.
(1)求 ;
;
(2)若数列 的公比
的公比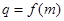 ,数列
,数列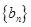 满足
满足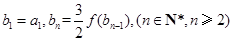 ,求证:
,求证: 为等差数列,并求
为等差数列,并求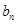 ;
;
(3)设数列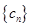 满足
满足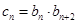 ,
,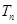 为数列
为数列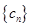 的前
的前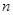 项和,且存在实数
项和,且存在实数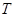 满足
满足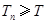 ,
, ,求
,求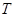 的最大值.
的最大值.
(本小题满分14分)如图1,在正三角形ABC中,AB=3,E、F、P分别是AB、AC、BC边上的点,AE=CF=CP=1. 将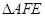 沿EF折起到
沿EF折起到 的位置,使平面
的位置,使平面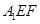 与平面BCFE垂直,连结A1B、A1P(如图2).
与平面BCFE垂直,连结A1B、A1P(如图2).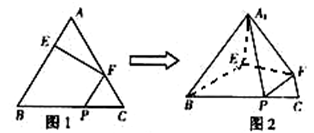
(1)求证:PF//平面A1EB;
(2)求证:平面 平面A1EB;
平面A1EB;
(3)求四棱锥A1—BPFE的体积.
(本小题满分12分)
在某次测验中,有6位同学的平均成绩为75分.用xn表示编号为n(n="1," 2,…,6)的同学所得成绩,且前5位同学的成绩如下:
| 编号n |
1 |
2 |
3 |
4 |
5 |
| 成绩xn |
70 |
76 |
72 |
70 |
72 |
(1)求第6位同学的成绩x6,及这6位同学成绩的标准差s;
(2)从前5位同学中,随机地选2位同学,求恰有1位同学成绩在区间(68,75)中的概率.