某部队进行射击训练,每个学员最多只能射击4次,学员如有2次命中目标,那么就不再继续射击。假设某学员每次命中目标的概率都是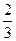 ,每次射击互相独立。
,每次射击互相独立。
(1)求该学员在前两次射击中至少有一次命中目标的概率;
(2)记该学员射击的次数为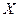 ,求
,求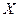 的分布列及数学期望。
的分布列及数学期望。
在 中,角A,B,C所对的边分别为
中,角A,B,C所对的边分别为
(Ⅰ)叙述并证明正弦定理;
(Ⅱ)设 ,
, ,求
,求 的值.
的值.
已知在等比数列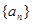 中,
中,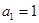 ,且
,且 是
是 和
和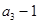 的等差中项.
的等差中项.
(Ⅰ)求数列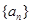 的通项公式;
的通项公式;
(Ⅱ)若数列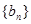 满足
满足 ,求
,求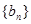 的前
的前 项和
项和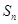 .
.
已知函数 ,
,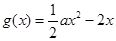 .
.
(Ⅰ)若曲线 在
在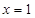 与
与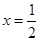 处的切线相互平行,求
处的切线相互平行,求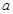 的值及切线斜率;
的值及切线斜率;
(Ⅱ)若函数 在区间
在区间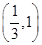 上单调递减,求
上单调递减,求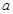 的取值范围;
的取值范围;
(Ⅲ)设函数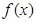 的图像C1与函数
的图像C1与函数 的图像C2交于P、Q两点,过线段PQ的中点作x轴的垂线分别交C1、C2于点M、N,证明:C1在点M处的切线与C2在点N处的切线不可能平行.
的图像C2交于P、Q两点,过线段PQ的中点作x轴的垂线分别交C1、C2于点M、N,证明:C1在点M处的切线与C2在点N处的切线不可能平行.
已知椭圆C的中心在坐标原点,短轴长为4,且有一个焦点与抛物线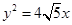 的焦点重合.
的焦点重合.
(Ⅰ)求椭圆C的方程;
(Ⅱ)已知经过定点M(2,0)且斜率不为0的直线 交椭圆C于A、B两点,试问在x轴上是否另存在一个定点P使得
交椭圆C于A、B两点,试问在x轴上是否另存在一个定点P使得 始终平分
始终平分 ?若存在求出
?若存在求出 点坐标;若不存在请说明理由.
点坐标;若不存在请说明理由.
如图,四棱锥S-ABCD中,SD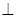 底面ABCD,AB//DC,AD
底面ABCD,AB//DC,AD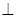 DC,AB=AD=1,DC=SD=2,E为棱SB上任一点.
DC,AB=AD=1,DC=SD=2,E为棱SB上任一点.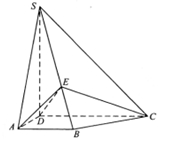
(Ⅰ)求证:无论E点取在何处恒有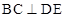 ;
;
(Ⅱ)设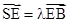 ,当平面EDC
,当平面EDC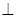 平面SBC时,求
平面SBC时,求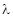 的值;
的值;
(Ⅲ)在(Ⅱ)的条件下求二面角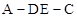 的大小.
的大小.