2014年索契冬季奥运会,已经在2014年02月07日至02月23日在俄罗斯联邦索契市举行。某校为了普及冬奥会的知识,举办知识竞赛活动.参与者需先后回答两道选择题,问题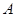 有三个选项,问题
有三个选项,问题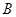 有四个选项,但都只有一个选项是正确的,正确回答问题
有四个选项,但都只有一个选项是正确的,正确回答问题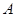 可获奖金
可获奖金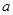 元,正确回答问题
元,正确回答问题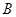 可获奖金
可获奖金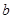 元,活动规定:参与者可任意选择回答问题的顺序,如果第一个问题回答正确,则继续答题,否则该参与者活动终止,假设一个参与者在回答问题前,对这两个问题都很陌生.
元,活动规定:参与者可任意选择回答问题的顺序,如果第一个问题回答正确,则继续答题,否则该参与者活动终止,假设一个参与者在回答问题前,对这两个问题都很陌生.
(1)如果参与者先回答问题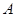 ,求其恰好获得奖金
,求其恰好获得奖金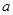 元的概率;
元的概率;
(2)试确定哪种回答问题的顺序能使该参与者获奖金额的期望值较大.
在 中,
中, 分别是内角
分别是内角 的对边,且
的对边,且
 ,且
,且 .
.
(1)求角 的大小;
的大小;
(2)若 边上高为1,求
边上高为1,求 面积的最小值.
面积的最小值.
已知1,2,…,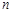 满足下列性质T的排列
满足下列性质T的排列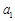 ,
,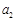 ,…,
,…,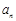 的个数为
的个数为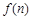 (n≥2,且n∈N*).
(n≥2,且n∈N*).
性质T:排列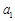 ,
,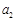 ,…,
,…,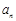 中有且只有一个
中有且只有一个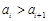 (
(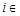 {1,2,…,
{1,2,…,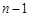 }).
}).
(1)求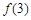 ;
;
(2)求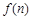 .
.
从棱长为1的正方体的8个顶点中任取不同2点,设随机变量ξ是这两点间的距离.
(1)求概率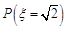 ;
;
(2)求ξ的分布列,并求其数学期望E(ξ).
已知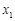 ,
,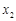 ,
,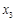 为正实数,若
为正实数,若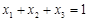 ,求证:
,求证: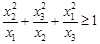 .
.