已知f(x)=loga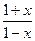 (a>0,a≠1).
(a>0,a≠1).
(1)求f(x)的定义域;(2)判断f(x)的奇偶性并证明.
甲、乙两名运动员在一次射击预选赛中,分别射击了4次,成绩如下表(单位:环):
| 甲 |
6 |
7 |
9 |
10 |
| 乙 |
6 |
8 |
8 |
10 |
(Ⅰ)从甲、乙两人的成绩中各随机抽取一个,求甲的成绩比乙高的概率;
(Ⅱ)现要从中选派一人参加正式比赛,你认为选派哪位运动员参加比较合适?请说明理由.
在等差数列{an}中,Sn为其前n项和,且a5=9,S3=9.
(Ⅰ)求数列{an}的通项an;
(Ⅱ)若数列{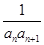 }的前n项和为Tn,求2Tn≥
}的前n项和为Tn,求2Tn≥ 的最小正整数n的值.
的最小正整数n的值.
已知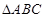 的顶点
的顶点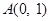 ,
,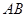 边上的中线
边上的中线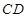 所在的直线方程为
所在的直线方程为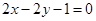 ,
, 边上的高
边上的高 所在直线的方程为
所在直线的方程为 。
。
(1)求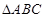 的顶点
的顶点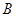 、
、 的坐标;
的坐标;
(2)若圆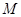 经过不同的三点
经过不同的三点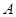 、
、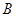 、
、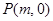 ,且斜率为
,且斜率为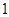 的直线与圆
的直线与圆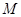 相切于点
相切于点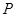 ,求圆
,求圆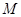 的方程;
的方程;
(3)问圆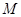 是否存在斜率为
是否存在斜率为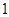 的直线
的直线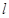 ,使
,使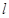 被圆
被圆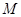 截得的弦为
截得的弦为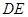 ,以
,以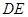 为直径的圆经过原点.若存在,写出直线
为直径的圆经过原点.若存在,写出直线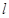 的方程;若不存在,说明理由。
的方程;若不存在,说明理由。
设命题 :方程
:方程 无实数根;命题
无实数根;命题 :函数
:函数 的值域是
的值域是 .如果命题
.如果命题 为真命题,
为真命题, 为假命题,求实数
为假命题,求实数 的取值范围。
的取值范围。
为了让学生了解环保知识,增强环保意识,某中学举行了一次“环保知识竞赛”,共有1000名学生参加了这次竞赛.为了了解本次竞赛成绩情况,从中抽取了部分学生的成绩(得分均为整数,满分为100分)进行统计.请你根据尚未完成的频率分布表和频数分布条形图,解答下列问题: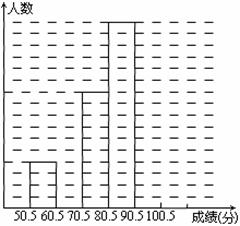
(1)求频率分布表中的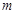 ,
,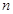 值,并补全频数条形图;
值,并补全频数条形图;
(2)根据频数条形图估计该样本的中位数是多少?
(3)若成绩在65.5~85.5分的学生为三等奖,问该校获得三等奖的学生约为多少人?