(本小题满分12分)
如图1,在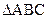 中,
中, °,BD
°,BD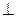 AC,AD=2CD=4,将
AC,AD=2CD=4,将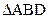 沿BD折起至
沿BD折起至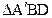 的位置,连结
的位置,连结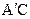 ,(如图2),记二面角
,(如图2),记二面角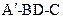 的大小为
的大小为 (0<
(0< <
<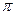 ).
).
(I) 求证:BD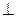
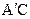 。
。
(II) 当 =90°时,求四面体
=90°时,求四面体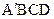 的表面积。
的表面积。
(本小题满分12分)已知等差数列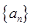 满足:
满足: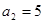 ,
,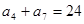 ,
,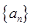 的前n项和为
的前n项和为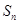 .
.
(Ⅰ)求通项公式 及前n项和
及前n项和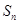 ;
;
(Ⅱ)令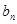 =
=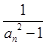 (n
(n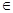 N*),求数列
N*),求数列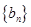 的前n项和
的前n项和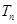 .
.
(本小题满分12分) 在△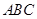 中,角A、B、C所对的边分别是
中,角A、B、C所对的边分别是 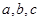 ,且
,且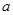 ="2,"
="2," 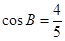 .
.
(Ⅰ)b="3," 求 的值.
的值.
(Ⅱ)若△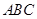 的面积
的面积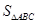 =3,求b,c的值.
=3,求b,c的值.
(本小题满分14分)已知数列 满足
满足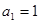 ,
,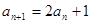 (
(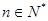 ).
).
(Ⅰ)求数列 的通项公式;
的通项公式;
(Ⅱ)若数列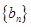 满足
满足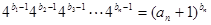 (
(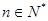 ),证明:数列
),证明:数列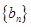 是等差数列;
是等差数列;
(Ⅲ)证明: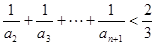 (
(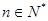 ).
).
如图,有一块边长为1(百米)的正方形区域ABCD,在点A处有一个可转动的探照灯,其照射角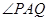 始终为
始终为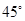 (其中点P,Q分别在边BC,CD上),设
(其中点P,Q分别在边BC,CD上),设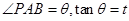 .
.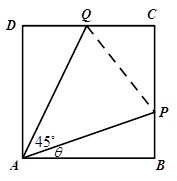

(Ⅰ)用t表示出PQ的长度,并探求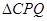 的周长l是否为定值;
的周长l是否为定值;
(Ⅱ)问探照灯照射在正方形ABCD内部区域阴影部分的面积S最大为多少(平方百米)?
我炮兵阵地位于地面A处,两观察所分别位于地面点C和D处,已知CD=6 ,∠ACD=45°,∠ADC=75°, 目标出现于地面点B处时,测得∠BCD=30°,∠BDC=15°(如图),求炮兵阵地到目标的距离.
,∠ACD=45°,∠ADC=75°, 目标出现于地面点B处时,测得∠BCD=30°,∠BDC=15°(如图),求炮兵阵地到目标的距离.