(本小题满分15分)
运货卡车以每小时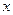 千米的速度匀速行驶130千米
千米的速度匀速行驶130千米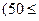
 (单位:千米/小时).假设汽油的价格是每升2元,而汽车每小时耗油
(单位:千米/小时).假设汽油的价格是每升2元,而汽车每小时耗油 升,司机的工资是每小时14元.
升,司机的工资是每小时14元.
(1)求这次行车总费用 关于
关于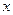 的表达式;
的表达式;
(2)当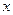 为何值时,这次行车的总费用最低,并求出最低费用的值.
为何值时,这次行车的总费用最低,并求出最低费用的值.
根据如图所示的程序框图,将输出的x、y值依次分别记为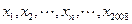 ;
;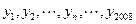
(Ⅰ)求数列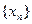 的通项公式
的通项公式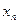 ;
;
(Ⅱ)写出y1,y2,y3,y4,由此猜想出数列{yn}的一个通项公式yn,并证明你的结论;
(Ⅲ)求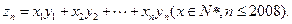

已知函数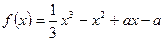 (
(
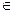 R).
R).
(Ⅰ )当
)当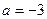 时,求函数
时,求函数 的极值;
的极值;
(Ⅱ)若函数 的图象与
的图象与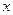 轴有且只有一个交点,求
轴有且只有一个交点,求 的取值范围.
的取值范围.
如图,在三棱拄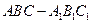 中,
中,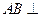 侧面
侧面 ,
,
已知

(Ⅰ)试在棱 (不包含端点
(不包含端点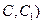 上确定一点
上确定一点 的位置,使得
的位置,使得 ;
; (Ⅱ) 在(Ⅰ)的条件下,求二面角
(Ⅱ) 在(Ⅰ)的条件下,求二面角 的平面角的正切值.
的平面角的正切值.
一厂家向用户提供的一箱产品共10件,其中有2件次品,用户先对产品进行抽检以决定是否接收.抽检规则是这样的:一次取一件产品检查(取出的产品不放回箱子),若前三次没有抽查到次品,则用户接收这箱产品;若前三次中一抽查到次品就立即停止抽检,并且用户拒绝接收这箱产品.
(Ⅰ)求这箱产品被用户接收的概率;
(Ⅱ)记抽检的产品件数为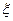 ,求
,求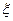 的分布列和数学期望.
的分布列和数学期望.
在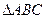 中,
中,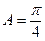 ,
,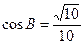 .
.
(Ⅰ)求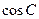 ;
;
(Ⅱ)设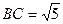 ,求
,求 的值.
的值.