本小题满分14分)
已知曲线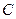 的极坐标方程为
的极坐标方程为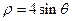 ,以极点为原点,极轴为
,以极点为原点,极轴为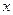 轴的非负半轴建立平面直角坐标系,直线
轴的非负半轴建立平面直角坐标系,直线 的参数方程为
的参数方程为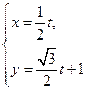 (
( 为参数),求直线
为参数),求直线 被曲线
被曲线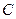 截得的线段的长度
截得的线段的长度
如图,在△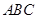 中,
中,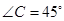 ,
,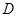 为
为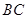 中点,
中点,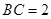 .记锐角
.记锐角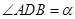 .且满足
.且满足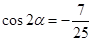 .
.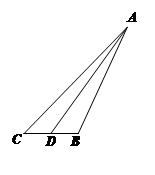
(1)求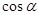 ;
;
(2)求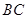 边上高的值.
边上高的值.
定义域为 的函数
的函数 ,其导函数为
,其导函数为 .若对
.若对 ,均有
,均有 ,则称函数
,则称函数 为
为 上的梦想函数.
上的梦想函数.
(Ⅰ)已知函数 ,试判断
,试判断 是否为其定义域上的梦想函数,并说明理由;
是否为其定义域上的梦想函数,并说明理由;
(Ⅱ)已知函数 (
( ,
, )为其定义域上的梦想函数,求
)为其定义域上的梦想函数,求 的取值范围;
的取值范围;
(Ⅲ)已知函数 (
( ,
, )为其定义域上的梦想函数,求
)为其定义域上的梦想函数,求 的最大整数值.
的最大整数值.
已知 是中心在坐标原点
是中心在坐标原点 的椭圆
的椭圆 的一个焦点,且椭圆
的一个焦点,且椭圆 的离心率
的离心率 为
为 .
.
(Ⅰ)求椭圆 的方程;
的方程;
(Ⅱ)设: 、
、 为椭圆
为椭圆 上不同的点,直线
上不同的点,直线 的斜率为
的斜率为 ;
; 是满足
是满足 (
( )的点,且直线
)的点,且直线 的斜率为
的斜率为 .
.
①求 的值;
的值;
②若 的坐标为
的坐标为 ,求实数
,求实数 的取值范围.
的取值范围.
已知长方体 中,底面
中,底面 为正方形,
为正方形, 面
面 ,
, ,
, ,点
,点 在棱
在棱 上,且
上,且 .
.
(Ⅰ)试在棱 上确定一点
上确定一点 ,使得直线
,使得直线 平面
平面 ,并证明;
,并证明;
(Ⅱ)若动点 在底面
在底面 内,且
内,且 ,请说明点
,请说明点 的轨迹,并探求
的轨迹,并探求 长度的最小值.
长度的最小值.
在数列 和等比数列
和等比数列 中,
中, ,
, ,
, .
.
(Ⅰ)求数列 及
及 的通项公式;
的通项公式;
(Ⅱ)若 ,求数列
,求数列 的前
的前 项和
项和 .
.