(本小题满分10分)
已知,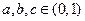 ,求证:
,求证: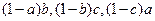 不能同时大于
不能同时大于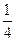 。
。
已知二次函数h(x)=ax2+bx+c(c>0),其导函数y=h′(x)的图象如下,且f(x)=ln x-h(x).
(1)求函数f(x)在x=1处的切线斜率;
(2)若函数f(x)在上是单调函数,求实数m的取值范围;
(3)若函数y=2x-lnx(x∈[1,4])的图象总在函数y=f(x)的图象的上方,求c的取值范围.
规定A =x(x-1)…(x-m+1),其中x∈R,m为正整数,且A
=x(x-1)…(x-m+1),其中x∈R,m为正整数,且A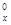 =1,这是排列数A
=1,这是排列数A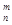 (n,m是正整数,且m≤n)的一种推广.
(n,m是正整数,且m≤n)的一种推广.
(1)求A 的值;
的值;
(2)排列数的性质:A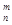 =nA
=nA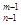 (其中m,n是正整数).问是否都能推广到A
(其中m,n是正整数).问是否都能推广到A (x∈R,m是正整数)的情形?若能推广,写出推广的形式,并且给予证明。
(x∈R,m是正整数)的情形?若能推广,写出推广的形式,并且给予证明。
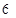 个人坐在一排
个人坐在一排 个座位上,问
个座位上,问
(1)空位不相邻的坐法有多少种?(用数字作答)
(2) 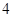 个空位只有
个空位只有 个相邻的坐法有多少种? (用数字作答)
个相邻的坐法有多少种? (用数字作答)
(3) 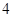 个空位至多有
个空位至多有 个相邻的坐法有多少种? (用数字作答)
个相邻的坐法有多少种? (用数字作答)
已知函数 ,其中
,其中 是常数.
是常数. (1)当
(1)当 时,求曲线
时,求曲线 在点
在点 处的切线方程;
处的切线方程;
(2)若存在实数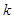 ,使得关于
,使得关于 的方程
的方程 上有两个不相等的实数根,求
上有两个不相等的实数根,求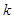 的取值范围.
的取值范围.
用数学归纳法证明:
当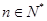 时,
时, 成立
成立