本题满分12分)在一个盒子中装有6支圆珠笔,其中3支一等品,2支二等品和1支三等品,从中任取3支﹒求
(Ⅰ)恰有1支一等品的概率;
(Ⅱ)没有三等品的概率﹒
已知矩形中ABCD,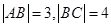 ,
,
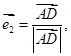
(1)若 ,求
,求
(2)求 与
与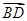 夹角的余弦值.
夹角的余弦值.
已知二次函数f(x)=ax2+bx+c(a>0).
(Ⅰ)(i)若b=﹣2,且f(x)在(1,+∞)上为单调递增函数,求实数a的取值范围;
(ii)若b=﹣1,c=1,当x∈[0,1]时,|f(x)|的最大值为1,求实数a的取值范围;
(Ⅱ)若f(0)≥1,f(1)≥1,f(x)=0的有两个小于1的不等正根,求a的最小正整数值.
已知抛物线C:y2=2x,O为坐标原点,经过点M(2,0)的直线l交抛物线于A,B两点,P为抛物线C上一点.
(Ⅰ)若直线l垂直于x轴,求| ﹣
﹣ |的值;
|的值;
(Ⅱ)求三角形OAB的面积S的取值范围.
如图,已知三角形△ABC与△BCD所在平面相互垂直,且∠BAC=∠BCD=90°,AB=AC,CB=CD,点P,Q分别在线段BD,CD上,沿直线PQ将△PQD向上翻折,使D与A重合.
(Ⅰ)求证:AB⊥CQ;
(Ⅱ)求BP的长;
(Ⅲ)求直线AP与平面BCD所成的角.
已知a,b,c分别为△ABC三个内角A,B,C的对边,a2=b2+c2﹣bc.
(Ⅰ)求A;
(Ⅱ)若a=2,求bsinB+csinC的最大值.