(本题满分12分).设函数f(x)= ·,其中向量=(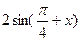 ,
, ),
),
 =(
=(
 ,
, ),x
),x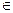 R求:
R求:
(1)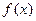 的解析式并进行化简;
的解析式并进行化简;
(2)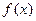 的周期和单调递增区间;
的周期和单调递增区间;
(3)若关于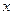 的方程
的方程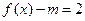 在
在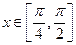 上有解,求实数
上有解,求实数 的取值范围。
的取值范围。
(本小题共12分)设向量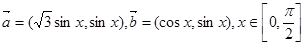
(1)若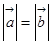 ,求x的值;
,求x的值;
(2)设函数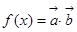 ,求
,求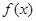 的最大值.
的最大值.
(本小题共10分)已知函数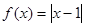
(1)解关于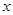 的不等式
的不等式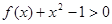 ;
;
(2)若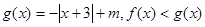 的解集非空,求实数
的解集非空,求实数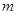 的取值范围.
的取值范围.
(本小题满分16分)在数列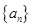 中,
中,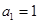 ,
,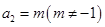 ,前
,前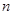 项和
项和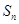 满足
满足 .
.
(1)求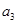 (用
(用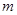 表示);
表示);
(2)求证:数列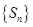 是等比数列;
是等比数列;
(3)若 ,现按如下方法构造项数为
,现按如下方法构造项数为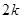 的有穷数列
的有穷数列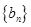 :当
:当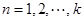 时,
时,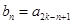 ;当
;当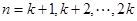 时,
时,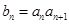 ,记数列
,记数列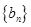 的前
的前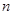 项和
项和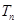 ,试问:
,试问: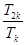 是否能取整数?若能,请求出
是否能取整数?若能,请求出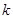 的取值集合;若不能,请说明理由.
的取值集合;若不能,请说明理由.
(本小题满分16分)在平面直角坐标系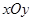 中,圆
中,圆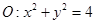 交
交 轴于点
轴于点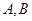 (点
(点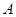 在
在 轴的负半轴上),点
轴的负半轴上),点 为圆
为圆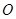 上一动点,
上一动点,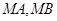 分别交直线
分别交直线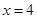 于
于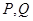 两点.
两点.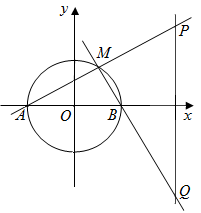
(1)求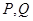 两点纵坐标的乘积;
两点纵坐标的乘积;
(2)若点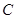 的坐标为
的坐标为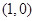 ,连接
,连接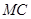 交圆
交圆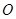 于另一点
于另一点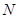 .
.
①试判断点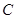 与以
与以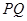 为直径的圆的位置关系,并说明理由;
为直径的圆的位置关系,并说明理由;
②记 的斜率分别为
的斜率分别为 ,试探究
,试探究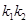 是否为定值?若是,请求出该定值;若不是,请说明理由.
是否为定值?若是,请求出该定值;若不是,请说明理由.
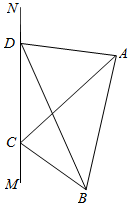
(本小题满分16分)如图,为对某失事客轮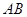 进行有效援助,现分别在河岸
进行有效援助,现分别在河岸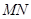 选择两处
选择两处 、
、 用强光柱进行辅助照明,其中
用强光柱进行辅助照明,其中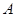 、
、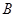 、
、 、
、 在同一平面内.现测得
在同一平面内.现测得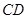 长为
长为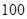 米,
米,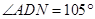 ,
,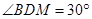 ,
,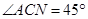 ,
,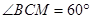 .
.
(1)求 的面积;
的面积;
(2)求船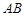 的长.
的长.