为了了解高中新生的体能情况,某学校抽取部分高一学生进行一分钟跳绳次数测试,将所得数据整理后,画出频率分布直方图(如图),图中从 左到右各小长方形面积之比为2:4:17:15:9:3,第二小组频数为12﹒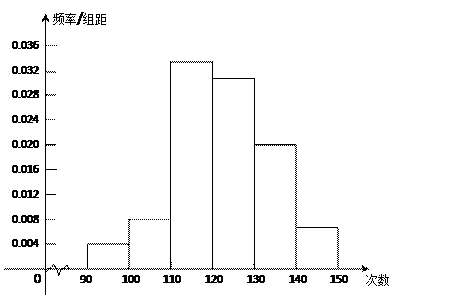
(Ⅰ)第二小组的频率是多少?样本容量是多少?
(Ⅱ)若次数在110以上(含110次)为达标,试估计该学校全体高一学生的达标率是多少?
(Ⅲ)在这次测试中,学生跳绳次数的中位数落在哪个小组内?请说明理由.
(本小题满分15分)如图,在三棱柱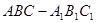 中,已知
中,已知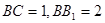 ,
,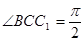 ,
, .
.
(Ⅰ)求直线 与底面
与底面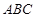 所成角正切值;
所成角正切值;
(Ⅱ)在棱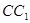 (不包含端点)上确定一点
(不包含端点)上确定一点 的位置,
的位置,
使得 (要求说明理由);
(要求说明理由);
(Ⅲ)在(Ⅱ)的条件下,若 ,求二面角
,求二面角 的大小.
的大小.
(本小题满分14分)已知椭圆 的中心在坐标原点,焦点在
的中心在坐标原点,焦点在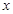 轴上,椭圆上的点到
轴上,椭圆上的点到
两个焦点的距离之和为 ,离心率
,离心率 .
.
(Ⅰ)求椭圆 的方程;
的方程;
(Ⅱ)设椭圆 的左、右焦点分别为
的左、右焦点分别为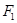 、
、 ,过点
,过点 的直线
的直线 与该椭圆交于点
与该椭圆交于点 、
、 ,
,
以 、
、 为邻边作平行四边形
为邻边作平行四边形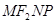 ,求该平行四边形对角线
,求该平行四边形对角线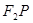 的长度
的长度
的最大值.
(本小题满分14分)如图,正方形 和四边形
和四边形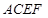 所在的平面互相垂直,
所在的平面互相垂直,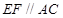 ,
,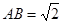 ,
,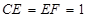 ,
,
(Ⅰ)求证: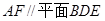 ;
;
(Ⅱ)求异面直线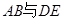 所成角的余弦值.
所成角的余弦值.
(本小题满分14分) 已知命题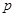 :存在
:存在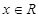 ,使
,使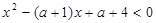 ;命题
;命题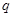 :方程
:方程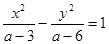 表示双曲线.若命题“
表示双曲线.若命题“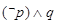 ”为真命题,求实数
”为真命题,求实数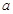 的取值范围.
的取值范围.
(长为3的线段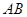 的两个端点
的两个端点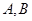 分别在
分别在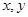 轴上移动,点
轴上移动,点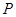 在直线
在直线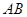 上且满足
上且满足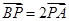 .(I)求点
.(I)求点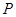 的轨迹的方程;(II)记点
的轨迹的方程;(II)记点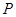 轨迹为曲线
轨迹为曲线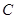 ,过点
,过点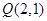 任作直线
任作直线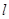 交曲线
交曲线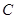 于
于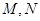 两点,过
两点,过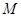 作斜率为
作斜率为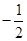 的直线
的直线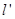 交曲线
交曲线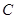 于另一点
于另一点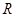 .求证:直线
.求证:直线 与直线
与直线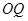 的交点为定点(
的交点为定点(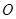 为坐标原点),并求出该定点.
为坐标原点),并求出该定点.