如图,Rt△ABC中,AC=BC= ,CD⊥AB,沿CD将△ABC折成600的二面角A―CD―B ,求折叠后点A到平面BCD的距离。
,CD⊥AB,沿CD将△ABC折成600的二面角A―CD―B ,求折叠后点A到平面BCD的距离。

 C. C
C. C
 D
D
A. D. B. A. B
若经过两点A(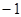 , 0),B(0, 2)的直线
, 0),B(0, 2)的直线 与圆
与圆 相切,求
相切,求 的值
的值
已知定义在R上的二次函数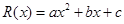 满足
满足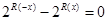 ,且
,且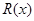 的最小值为0,函数
的最小值为0,函数 ,又函数
,又函数 。
。
(I)求 的单调区间;
的单调区间;
(II)当 ≤
≤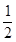 时,若
时,若 ,求
,求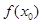 的最小值;
的最小值;
(III)若二次函数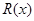 图象过(4,2)点,对于给定的函数
图象过(4,2)点,对于给定的函数 图象上的点A(
图象上的点A( ),当
),当 时,探求函数
时,探求函数 图象上是否存在点B(
图象上是否存在点B( )(
)(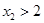 ),使A、B连线平行于x轴,并说明理由。
),使A、B连线平行于x轴,并说明理由。
(参考数据:e=2.71828…)
已知数列 是各项均不为0的等差数列,公差为d,
是各项均不为0的等差数列,公差为d, 为其前n项和,且满足
为其前n项和,且满足 。数列
。数列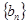 满足
满足 ,
, 为数列
为数列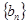 的前n项和。
的前n项和。
(I)求; d和
d和 ;
;
(II)若对任意的 ,不等式
,不等式 恒成立,求实数
恒成立,求实数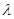 的取值范围。
的取值范围。
如图,某园林绿化单位准备在一直角ABC内的空地上植造一块“绿地△ABD”,规划在△ABD的内接正方形BEFG内种花,其余地方种草,若AB=a, ,种草的面积为
,种草的面积为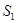 ,种花的面积为
,种花的面积为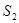 ,比值
,比值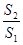 称为“规划和谐度”。
称为“规划和谐度”。
(I)试用 表示
表示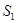 ,
,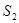 ;
;
(II)若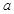 为定值,BC >AB。当
为定值,BC >AB。当 为何值时,“规划和谐度”有最小值?最小值是多少?
为何值时,“规划和谐度”有最小值?最小值是多少?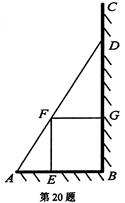
已知函数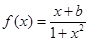 为奇函数。
为奇函数。
(I)证明:函数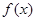 在区间(1,
在区间(1, )上是减函数;
)上是减函数;
(II)解关于x的不等式