已知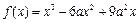 (
( ).
).
⑴求函数 的单调递减区间;
的单调递减区间;
⑵当 时,若对
时,若对 有
有 恒成立,求实数
恒成立,求实数 的取值范围.
的取值范围.
某工厂拟建一座平面图(如下图)为矩形且面积为200平方米的三级污水处理池,由于地形限制,长、宽都不能超过16米,如果池外周壁建造单价为每米400元,中间两条隔墙建造单价为每米248元,池底建造单价为每平方米80元(池壁厚度忽略不计,且池无盖).
(1)写出总造价y(元)与污水处理池长x(米)的函数关系式,并指出其定义域.
(2)求污水处理池的长和宽各为多少时,污水处理池的总造价最低?并求最低总造价. 
定义在(-1,1)上的函数f(x)满足①对任意x、y∈(-1,1),都有f(x)+f(y)=f(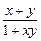 );②当x∈(-1,0)时,有f(x)>0.
);②当x∈(-1,0)时,有f(x)>0.
求证: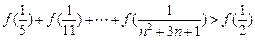 .
.
设f(x)=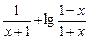 .
.
(1)证明:f(x)在其定义域上的单调性;
(2)证明: 方程f-1(x)=0有惟一解;
(3)解不等式f[x(x-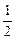 )]<
)]<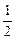 .
.
设a为实数,函数f(x)=x2+|x-a|+1,x∈R.
(1)讨论f(x)的奇偶性;(2)求f(x)的最小值.
(本题满分12分)
求两对称轴与坐标轴重合,离心率e=0.8,焦点到相应准线的距离等于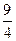 的椭圆方程.
的椭圆方程.