(本小题满分10分)选修4-4:坐标系与参数方程.
已知曲线C: 为参数,0≤
为参数,0≤ <2π),
<2π),
(Ⅰ)将曲线化为普通方程;
(Ⅱ)求出该曲线在以直角坐标系原点为极点, 轴非负半轴为极轴的极坐标系下的极坐标方程.
轴非负半轴为极轴的极坐标系下的极坐标方程.
(本小题满分12分)已知在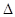 ABC中,内角A,B,C的对边分别为
ABC中,内角A,B,C的对边分别为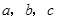 .且
.且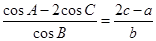 .
.
(Ⅰ)求 的值;
的值;
(Ⅱ)若 =
= ,b=2,求
,b=2,求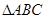 的面积S。
的面积S。
(本小题满分12分)已知数列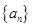 的通项公式为
的通项公式为 (
( ),且
),且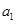 =-
=-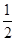 ,
, =-
=-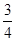 .
.
(1)求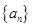 的通项公式;
的通项公式;
(2)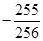 是否为数列
是否为数列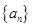 中的项,若是,是第几项?若不是请说明理由。
中的项,若是,是第几项?若不是请说明理由。
(3)该数列是递增数列还是递减数列?
(本小题满分12分)已知函数f(x)= sin xcos x-
sin xcos x- cos2x
cos2x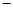

(1)求f(x)的最小正周期和单调递增区间;
(2)当x∈ 时,求函数f(x)的最大值和最小值及相应的x的值.
时,求函数f(x)的最大值和最小值及相应的x的值.
(本小题满分12分)已知在等差数列 中,
中,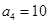 且
且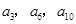 成等比数列,求数列
成等比数列,求数列 前20项的和
前20项的和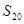 .
.
(本小题满分10分)已知 ,
, ,
, 的夹角为60o,
的夹角为60o,  ,
, ,
, ,求
,求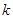 的值。
的值。