如图,在半径为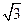 、圆心角为
、圆心角为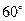 的扇形的弧上任取
的扇形的弧上任取 一点
一点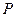 ,作扇
,作扇 形的内接矩形
形的内接矩形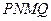 ,使点
,使点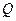 在
在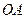 上,点
上,点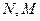 在
在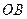 上,设矩形
上,设矩形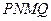 的面积为
的面积为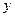 ,
,
(1)按下列要求写出函数的关系式:
① 设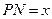 ,将
,将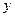 表示成
表示成 的函数关系式;
的函数关系式;
② 设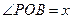 ,将
,将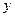 表
表 示成
示成 的函数关系式,
的函数关系式,
(2)请你选用(1)中的一个函数关系式,求出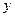 的最大值。
的最大值。
(本小题满分15分)已知直线l的方程为: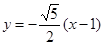 ,直线l与x轴的交点为F, 圆O的方程为:
,直线l与x轴的交点为F, 圆O的方程为: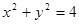 ,C、 D在圆上, CF⊥DF,设线段CD的中点为M.
,C、 D在圆上, CF⊥DF,设线段CD的中点为M.
(1)如果CFDG为平行四边形,求动点G的轨迹;
(2)已知椭圆的中心在原点,右焦点为F,直线l交椭圆于A、B两点,又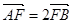 ,
,
求椭圆C的方程.
(本小题满分15分)
函数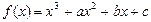 ,曲线
,曲线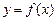 上点
上点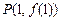 处的切线方程为
处的切线方程为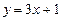
(1)若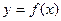 在
在 时有极值,求函数
时有极值,求函数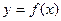 在
在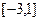 上的最大值;
上的最大值;
(2)若函数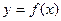 在区间
在区间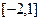 上单调递增,求
上单调递增,求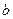 的取值范围.
的取值范围.
(本小题满分14分)
数列{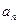 }满足递推式
}满足递推式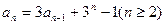 ,其中
,其中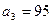 .
.
(1)求a1,a2;
(2)是否存在一个实数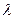 ,使得
,使得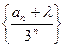 为等差数列,如果存在,求出
为等差数列,如果存在,求出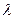 的值;如果不存在,试
的值;如果不存在,试
说明理由;
(3)求数列{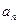 }的前n项之和.
}的前n项之和.
(本小题满分14分)
已知向量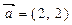 ,向量
,向量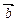 与
与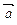 的夹角为
的夹角为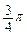 , 且
, 且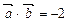 .
.
(1)求向量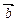 ;
;
(2)若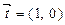 且
且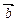
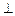
 ,
,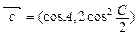 ,其中A、C是
,其中A、C是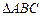 的内角,若三角形的三个内角A、B、C依次成等差数列,试求
的内角,若三角形的三个内角A、B、C依次成等差数列,试求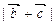 的取值范围
的取值范围
(本小题满分14分)
在锐角△ABC中,已知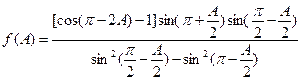 .
.
(1)求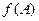 的最大值;
的最大值;
(2)当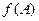 取得最大值时,
取得最大值时, ,如果
,如果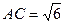 ,求
,求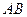 边和
边和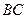 边的长.
边的长.