(本小题满分14分)
已知向量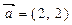 ,向量
,向量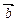 与
与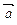 的夹角为
的夹角为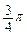 , 且
, 且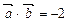 .
.
(1)求向量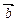 ;
;
(2)若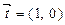 且
且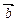
 ,
,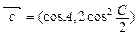 ,其中A、C是
,其中A、C是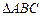 的内角,若三角形的三个内角A、B、C依次成等差数列,试求
的内角,若三角形的三个内角A、B、C依次成等差数列,试求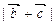 的取值范围
的取值范围
在锐角△ABC中,角A,B,C的对边分别为 .已知
.已知 .
.
(1)求B;
(2)若 ,
, ,求
,求 .
.
(本小题满分12分)已知函数 .
.
(1)当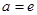 时,
时, ,
,
①求 的单调增区间;
的单调增区间;
②当 时,讨论曲线
时,讨论曲线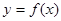 与
与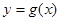 的交点个数.
的交点个数.
(2)若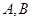 是曲线
是曲线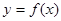 上不同的两点,点
上不同的两点,点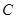 是弦
是弦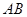 的中点,过点
的中点,过点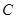 作
作 轴的垂线交曲线
轴的垂线交曲线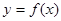 于点
于点 ,
,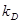 是曲线
是曲线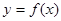 在点
在点 处的切线的斜率,试比较
处的切线的斜率,试比较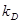 与
与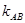 的大小.
的大小.
(本小题满分12分)设数列 的前
的前 项和为
项和为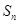 ,点
,点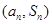 在直线
在直线 上.
上.
(1)求数列 的通项公式;
的通项公式;
(2)在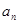 与
与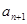 之间插入
之间插入 个数,使这
个数,使这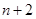 个数组成公差为
个数组成公差为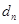 的等差数列,求数列
的等差数列,求数列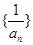 的前
的前 项和
项和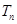 ,并求使
,并求使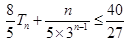 成立的正整数
成立的正整数 的最大值.
的最大值.
(本小题满分12分)已知 的顶点坐标为
的顶点坐标为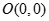 ,
, ,
,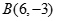 , 点P的横坐标为14,且
, 点P的横坐标为14,且 ,点
,点 是边
是边 上一点,且
上一点,且 .
.
(1)求实数 的值与点
的值与点 的坐标;
的坐标;
(2)求点 的坐标;
的坐标;
(3)若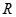 为线段
为线段 (含端点)上的一个动点,试求
(含端点)上的一个动点,试求 的取值范围.
的取值范围.
(本小题满分12分)数列 满足
满足 ,
, .
.
(1)求数列 的通项公式;
的通项公式;
(2)记 ,数列
,数列 的前
的前 项和是
项和是 ,证明:
,证明: .
.