已知圆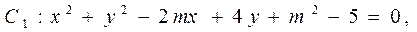 圆
圆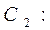
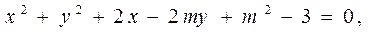 则
则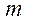 为何值时,
为何值时,
(1) 圆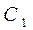 与圆
与圆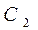 相切;
相切;
(2) 圆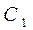 与圆
与圆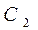 内含。
内含。
(本小题满分12分) 在 中,角
中,角 的对边分别是
的对边分别是 ,若
,若 .
.
(1)求角 的大小;
的大小;
(2)若 ,
, 的面积为
的面积为 ,求
,求 的值.
的值.
(本小题满分14分)已知二次函数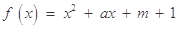 ,关于
,关于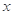 的不等式
的不等式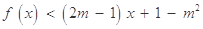 的解集为
的解集为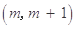 ,(
,(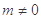 ),设
),设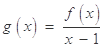 .
.
(1)求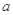 的值;
的值;
(2)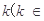 R
R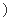 如何取值时,函数
如何取值时,函数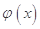
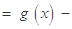
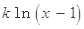 存在极值点,并求出极值点;
存在极值点,并求出极值点;
(3)若 ,且
,且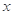
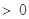 ,求证:
,求证: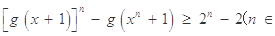 N
N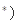 .
.
(本小题满分13分)已知椭圆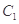 的中心在坐标原点,两个焦点分别为
的中心在坐标原点,两个焦点分别为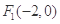 ,
,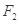
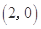 ,点
,点 在椭圆
在椭圆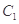 上,过点
上,过点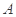 的直线
的直线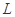 与抛物线
与抛物线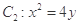 交于
交于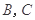 两点,抛物线
两点,抛物线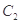 在点
在点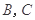 处的切线分别为
处的切线分别为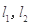 ,且
,且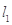 与
与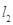 交于点
交于点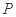 .
.
(1) 求椭圆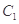 的方程;
的方程;
(2)是否存在满足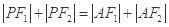 的点
的点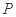 ? 若存在,指出这样的点
? 若存在,指出这样的点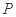 有几个(不必求出点
有几个(不必求出点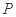 的坐标); 若不存在,说明理由.
的坐标); 若不存在,说明理由.
(本小题满分12分)如图,在正三棱柱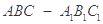 中,△
中,△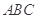 是边长为
是边长为 的等边三角形,
的等边三角形,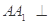 平面
平面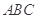 ,
,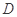 ,
,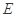 分别是
分别是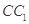 ,
,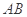 的中点.
的中点.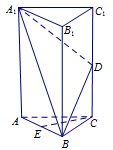
(1)求证: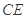 ∥平面
∥平面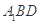 ;
;
(2)若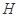 为
为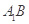 上的动点,当
上的动点,当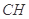 与平面
与平面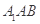 所成最大角的正切为
所成最大角的正切为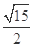 时,求平面
时,求平面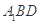 与平面
与平面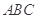 所成二面角(锐角)的余弦值.
所成二面角(锐角)的余弦值.
(本小题满分12分)已知数列 的前
的前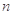 项和
项和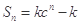 (其中
(其中 为常数),且
为常数),且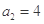 ,
, .
.
(1)求 ;
;
(2)求数列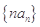 的前
的前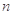 项和
项和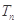 .
.