设 .
(Ⅰ)令
,讨论
在
内的单调性并求极值;
(Ⅱ)求证:当
时,恒有
.
市一中随机抽取部分高一学生调查其上学路上所需时间(单位:分钟),并将所得数据绘制成频率分布直方图(如图),其中上学路上所需时间的范围是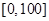 ,样本数据分组为
,样本数据分组为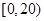 ,
,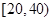 ,
,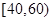 ,
,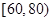 ,
,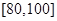 .
.
(Ⅰ)求直方图中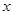 的值;
的值;
(Ⅱ)如果上学路上所需时间不少于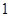 小时的学生可申请在学校住宿,若招生
小时的学生可申请在学校住宿,若招生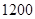 名,请估计新生中有多少名学生可以申请住宿;
名,请估计新生中有多少名学生可以申请住宿;
(Ⅲ)从学校的高一学生中任选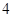 名学生,这
名学生,这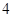 名学生中上学路上所需时间少于
名学生中上学路上所需时间少于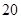 分钟的人数记为
分钟的人数记为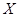 ,求
,求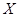 的分布列和数学期望.(以直方图中的频率作为概率)
的分布列和数学期望.(以直方图中的频率作为概率)
已知数列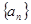 的各项均为正数,前
的各项均为正数,前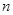 项和为
项和为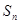 ,且
,且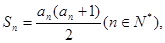
(Ⅰ)求证数列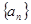 是等差数列;
是等差数列;
(Ⅱ)设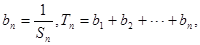 求
求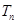 .
.
(本小题满分14分)设函数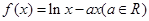 (e=2.718 28是自然对数的底数).
(e=2.718 28是自然对数的底数).
(1)当 时,求
时,求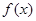 在点
在点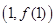 处的切线方程;
处的切线方程;
(2)判断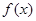 的单调性;
的单调性;
(3)证明:当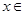 (1,+∞)时,
(1,+∞)时,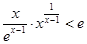 .
.
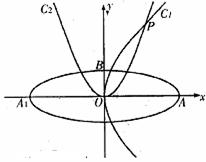
(本小题满分12分)如图,椭圆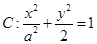
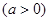 的焦点在
的焦点在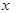 轴上,左右顶点分别为
轴上,左右顶点分别为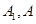 ,上顶点为
,上顶点为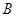 ,抛物线
,抛物线 分别以
分别以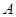 、
、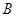 为焦点,其顶点均为坐标原点
为焦点,其顶点均为坐标原点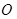 ,
,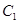 与
与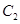 相交于直线
相交于直线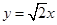 上一点
上一点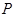 .
.
(1)求椭圆 及抛物线
及抛物线 的方程;
的方程;
(2)若动直线 与直线
与直线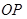 垂直,且与椭圆
垂直,且与椭圆 交于不同的两点
交于不同的两点 ,已知点
,已知点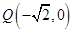 ,求
,求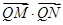 的最小值.
的最小值.
(本小题共12分)如图,PA 平面ABCD,四边形ABCD为矩形,PA=AB=
平面ABCD,四边形ABCD为矩形,PA=AB=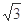 ,AD=1,点F是PB的中点,点E在边BC上移动.
,AD=1,点F是PB的中点,点E在边BC上移动.
(1)当点E为BC的中点时, 证明EF//平面PAC;
(2)求三棱锥E-PAD的体积;
(3)证明:无论点E在边BC的何处,都有PE AF.
AF.