某国采用养老储备金制度.公民在就业的第一年就交纳养老储备金,数目为 ,以后每年交纳的数目均比上一年增加 ,因此,历年所交纳的储务金数目 , ,…是一个公差为 的等差数列,与此同时,国家给予优惠的计息政策,不仅采用固定利率,而且计算复利.这就是说,如果固定年利率为 ,那么,在第 年末,第一年所交纳的储备金就变为 ,第二年所交纳的储备金就变为 ,……,以 表示到第 年末所累计的储备金总额.
(Ⅰ)写出
与
的递推关系式;
(Ⅱ)求证:
,其中
是一个等比数列,
是一个等差数列.
(本小题满分12分)在△ABC中,已知A=45°,cosB = .
.
(I)求cosC的值;
(11)若BC=" 10" , D为AB的中点,求CD的长.
(本小题满分14分)如图,已知直线OP1,OP2为双曲线E: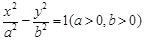 的渐近线,△P1OP2的面积为
的渐近线,△P1OP2的面积为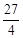 ,在双曲线E上存在点P为线段P1P2的一个三等分点,且双曲线E的离心率为
,在双曲线E上存在点P为线段P1P2的一个三等分点,且双曲线E的离心率为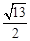 .
.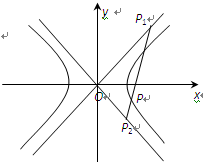
(1)若P1、P2点的横坐标分别为x1、x2,则x1、x2之间满足怎样的关系?并证明你的结论;
(2)求双曲线E的方程;
(3)设双曲线E上的动点 ,两焦点
,两焦点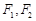 ,若
,若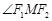 为钝角,求
为钝角,求 点横坐标
点横坐标 的取值范围.
的取值范围.
(本小题满分14分)已知函数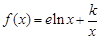 (其中e是自然对数的底数,k为正数)
(其中e是自然对数的底数,k为正数)
(1)若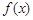 在
在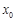 处取得极值,且
处取得极值,且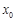 是
是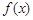 的一个零点,求k的值;
的一个零点,求k的值;
(2)若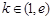 ,求
,求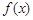 在区间
在区间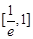 上的最大值.
上的最大值.
(本小题满分13分)如图是某直三棱柱(侧棱与底面垂直)被削去上底后的直观图与三视图的侧视图,俯视图,在直观图中,M是BD的中点,N是BC的中点,侧视图是直角梯形,俯视图是等腰直角三角形,有关数据如图所示.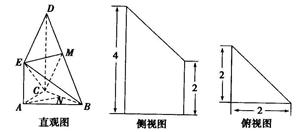
(1)求该几何体的体积;
(2)求证:AN∥平面CME;
(3)求证:平面BDE⊥平面BCD
(本小题满分12分)已知命题P:函数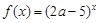 是R上的减函数,命题Q:在
是R上的减函数,命题Q:在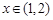 时,不等式
时,不等式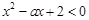 恒成立,若命题“
恒成立,若命题“ ”是真命题,求实数
”是真命题,求实数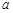 的取值范围.
的取值范围.