证明(1) 已知 ,求证
,求证 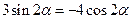
(2)已知数列 计算
计算 由此推算
由此推算 的公式,并用数学归纳法给出证明。
的公式,并用数学归纳法给出证明。
(本小题满分12分)已知圆C过点P(1,1),且与圆M: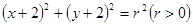 关于直线
关于直线 对称.
对称.
(1)求圆C的方程:
(2)设Q为圆C上的一个动点,求 最小值;
最小值;
(3)过点P作两条相异直线分别与圆C交与A,B,且直线PA和直线PB的倾斜角互补,O为坐标原点,试判断直线OP与直线AB是否平行?请说明理由.
(本小题满分12分)在平面直角坐标系 中,点
中,点 ,直线
,直线 ,设圆
,设圆 的半径为1,圆心在
的半径为1,圆心在 上.
上.
(1)若圆心 也在直线
也在直线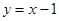 上,过点
上,过点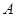 作圆
作圆 的切线,求切线的方程;
的切线,求切线的方程;
(2)若圆 上存在点
上存在点 ,使
,使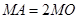 ,求圆心
,求圆心 的横坐标
的横坐标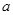 的取值范围.
的取值范围.
(本小题满分12分)设数列 的各项均为正数,它的前
的各项均为正数,它的前 项的和为
项的和为 ,点
,点 在函数
在函数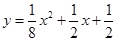 的图像上;数列
的图像上;数列 满足
满足 .其中
.其中 .
.
(1)求数列 和
和 的通项公式;
的通项公式;
(2)设 ,求证:数列
,求证:数列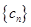 的前
的前 项的和
项的和 (
( ).
).
(本小题满分12分)已知函数
(1)当 时,求函数
时,求函数 的最小值和最大值;
的最小值和最大值;
(2)设 的内角
的内角 的对应边分别为
的对应边分别为 ,且
,且 ,若向量
,若向量 与向量
与向量 共线,求
共线,求 的值.
的值.
已知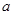 为实数,函数
为实数,函数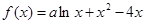 .
.
(1)当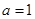 时,求
时,求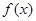 在
在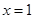 处的切线方程;
处的切线方程;
(2)定义:若函数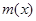 的图象上存在两点
的图象上存在两点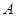 、
、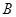 ,设线段
,设线段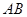 的中点为
的中点为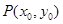 ,若
,若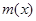 在点
在点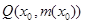 处的切线
处的切线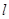 与直线
与直线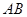 平行或重合,则函数
平行或重合,则函数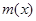 是“中值平衡函数”,切线
是“中值平衡函数”,切线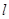 叫做函数
叫做函数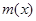 的“中值平衡切线”.试判断函数
的“中值平衡切线”.试判断函数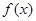 是否是“中值平衡函数”?若是,判断函数
是否是“中值平衡函数”?若是,判断函数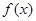 的“中值平衡切线”的条数;若不是,说明理由;
的“中值平衡切线”的条数;若不是,说明理由;
()设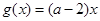 ,若存在
,若存在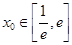 ,使得
,使得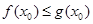 成立,求实数
成立,求实数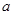 的取值范围.
的取值范围.