若椭圆 :
: 的离心率等于
的离心率等于 ,抛物线
,抛物线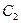 :
: 的焦点在椭圆的顶点上。
的焦点在椭圆的顶点上。
(1)求抛物线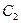 的方程;
的方程;
(2)求过点 的直线
的直线 与抛物线
与抛物线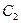 交
交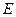 、
、 两点,又过
两点,又过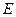 、
、 作抛物线
作抛物线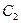 的切线
的切线 、
、 ,当
,当 时,求直线
时,求直线 的方程。
的方程。
设 为部分正整数组成的集合,数列 的首项 ,前 项和为 .已知对任意整数 属于 ,当 时, 都成立。
(1)设
,
,求
的值;
(2)设
,求数列
的通项公式。
已知
,
是实数,函数
,
和
是
的导函数,若
在区间I上恒成立,则称
和
在区间I上单调性一致
(1)设
,若函数
和
在区间
上单调性一致,求实数
的取值范围;
(2)设
且
,若函数
和
在以
,
为端点的开区间上单调性一致,求
的最大值。
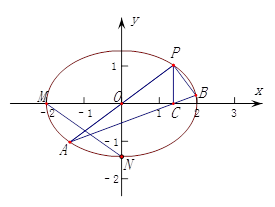
如图,在平面直角坐标系
中,
分别是椭圆
的顶点,过坐标原点的直线交椭圆于
两点,其中
在第一象限.过
作
轴的垂线,垂足为
.连接
,并延长交椭圆于点
.设直线
的斜率为
.
(Ⅰ)当直线
平分线段
时,求
的值;
(Ⅱ)当
时,求点
到直线
的距离;
(Ⅲ)对任意
,求证:
.
请你设计一个包装盒,如图所示, 是边长为60 的正方形硬纸片,切去阴影部分所示的四个全等的等腰直角三角形,再沿虚线折起,使得 四个点重合于图中的点 ,正好形成一个正四棱柱形状的包装盒, 在 上是被切去的等腰直角三角形斜边的两个端点,设 .


(1)若广告商要求包装盒侧面积
最大,试问
应取何值?
(2)若广告商要求包装盒容积
最大,试问
应取何值?并求出此时包装盒的高与底面边长的比值.
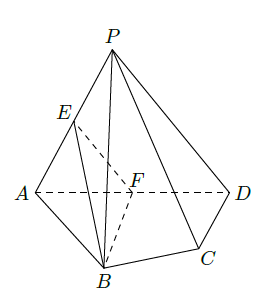
如图,在四棱锥
中,平面
平面
,
,
,
分别是
的中点.
求证:(1)直线
平面
;
(2)平面
平面
.