(本题12分)
已知函数 的定义域为集合A,函数
的定义域为集合A,函数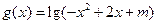 的定义域为集合B
的定义域为集合B
(1)当m=3时,求
(2)若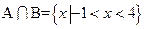 ,求实数m的值
,求实数m的值
(本小题满分12分)
设二次函数 在
在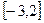 上有最大值4,求实数a的值。
上有最大值4,求实数a的值。
(本题12分)如图,已知△ABC是边长为1的正三角形,M、N分别是
边AB、AC上的点,线段MN经过△ABC的中心G,设ÐMGA=a(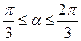 )
)
(1)试将△AGM、△AGN的面积(分别记为S1与S2)表示为a的函数
(2)求y=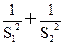 的最大值与最小值
的最大值与最小值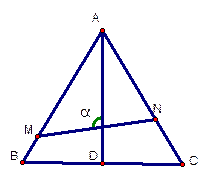
(本题12分)已知向量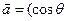 ,
,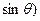 ,
,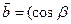 ,
,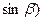 ,且
,且 与
与 之间有关系式:
之间有关系式: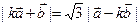 ,其中k>0.
,其中k>0.
(1)试用k表示 ;(2)求
;(2)求 的最小值,并求此时
的最小值,并求此时 与
与 的夹角
的夹角 的值.
的值.
(本题12分)已知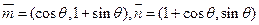
(1)如果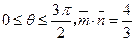 ,求
,求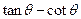 的值;(2)如果
的值;(2)如果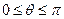 ,求
,求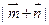 的取值范围.
的取值范围.
(本题12分)如图,函数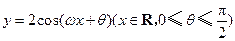 的图象与
的图象与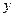 轴交于点
轴交于点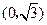 ,且最小正周期为π.
,且最小正周期为π.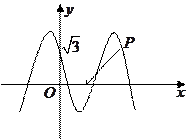
(1)求 和
和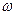 的值;(2)已知点
的值;(2)已知点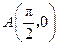 ,点
,点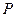 是该函数图象上一点,点
是该函数图象上一点,点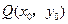 是
是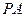 的中点,当
的中点,当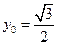 ,
,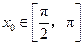 时,求
时,求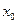 的值.
的值.