(本小题满分12分)
已知函数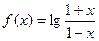 (Ⅰ)求证:对于
(Ⅰ)求证:对于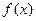 的定义域内的任意两个实数
的定义域内的任意两个实数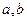 ,都有
,都有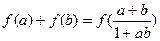 ;(Ⅱ)判断
;(Ⅱ)判断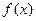 的奇偶性,并予以证明.
的奇偶性,并予以证明.
(本小题满分8分)某种产品的质量以其质量指标值衡量,质量指标值大于或等于98且小于106的产品为优质品,现用两种新配方(分别称为A配方和B配方)做试验,各生产了100件这种产品,并测量了每件产品的质量指标值,得到下面试验结果:
A配方的频数分布表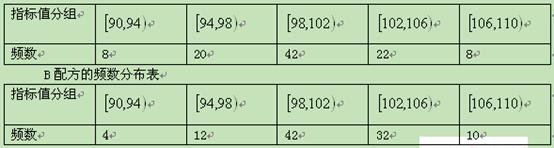
(Ⅰ)分别估计用A配方,B配方生产的产品的优质品率;
(Ⅱ)由以上统计数据填写2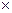 2列联表,问是否有99
2列联表,问是否有99 的把握认为“A配方与B配方的质量有差异”。
的把握认为“A配方与B配方的质量有差异”。
(本小题满分8分)
(Ⅰ)解不等式: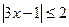 ;
;
(Ⅱ)设 ,
, ,
,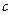
 ,求证:
,求证: .
.
已知函数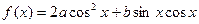 ,
, ,
,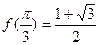
(1)求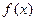 的最大值和最小值;
的最大值和最小值;
(2)求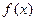 的单调递增区间
的单调递增区间
(3)对于角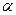 ,
, ,若有
,若有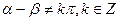 ,且
,且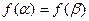 ,求
,求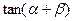 的值
的值
对甲、乙的学习成绩进行抽样分析,各抽5门功课,得到的观测值如下: 问:甲、乙谁的平均成绩最好?谁的各门功课发展较平衡?
问:甲、乙谁的平均成绩最好?谁的各门功课发展较平衡?
设函数
(1)求 的值;
的值;
(2)若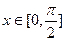 ,求
,求 的取值范围.
的取值范围.
(3)写出 对称中心.
对称中心.