(本小题满分12分)
已知m=(cosωx+sinωx, cosωx),n=(cosωx-sinωx,2sinωx),其中ω>0,若函数f(x)=m·n,且f(x)的对称中心到f(x)的对称轴的最近距离不小于
cosωx),n=(cosωx-sinωx,2sinωx),其中ω>0,若函数f(x)=m·n,且f(x)的对称中心到f(x)的对称轴的最近距离不小于 .
.
(I)求ω的取值范围;
(II)在△ABC中,a,b,c分别是内角A,B,C的对边,且a=1,b+c=2, 当ω取最大值时,f(A)=1,求△ABC的面积.
当ω取最大值时,f(A)=1,求△ABC的面积.
(本小题满分12分)
已知圆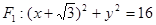 ,圆心为
,圆心为 ,定点
,定点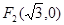 ,
,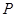 为圆
为圆 上一点,线段
上一点,线段 的垂直平分线与直线
的垂直平分线与直线 交于点
交于点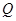 .
.
(Ⅰ)求点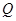 的轨迹
的轨迹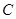 的方程;
的方程;
(Ⅱ)过点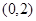 的直线
的直线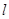 与曲线
与曲线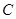 交于不同的两点
交于不同的两点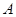 和
和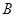 ,且满足
,且满足 (
( 为坐标原点),求直线
为坐标原点),求直线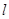 斜率的取值范围.
斜率的取值范围.
(本小题满分12分)
已知动点 在抛物线
在抛物线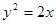 上,定点
上,定点 ,求
,求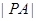 的最小值以及取最小值时
的最小值以及取最小值时 点的横坐标.
点的横坐标.
(本小题满分12分)
已知椭圆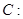
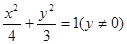 ,其左右焦点分别为
,其左右焦点分别为 .对于命题
.对于命题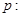 “
“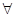 点
点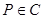 ,
,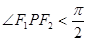 ”.写出
”.写出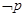 ,判断
,判断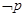 的真假,并说明理由.
的真假,并说明理由.
(本小题满分12分)
(Ⅰ)已知某椭圆的左右焦点分别为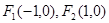 ,且经过点
,且经过点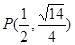 ,求该椭圆的标准方程;
,求该椭圆的标准方程;
(Ⅱ)某圆锥曲线以坐标轴为对称轴,中心为坐标原点,且过点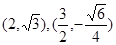 ,求该曲线的标准方程;
,求该曲线的标准方程;
(本小题满分10分)
已知命题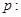 “
“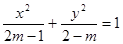 是椭圆的标准方程”,命题
是椭圆的标准方程”,命题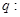 “
“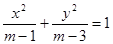 是双曲线的标准方程”.且
是双曲线的标准方程”.且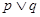 为真命题,
为真命题,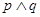 为假命题,求实数
为假命题,求实数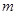 的取值范围.
的取值范围.