(本小题满分12分)
已知数列
(I)设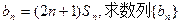 的通项公式;
的通项公式;
(II)当
(本小题满分14分)
在ΔABC中,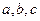 分别为
分别为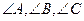 的对边,已知
的对边,已知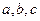 成等比数列,且
成等比数列,且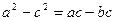 .求:
.求:
(Ⅰ)A的大小; (Ⅱ)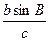 的值.
的值.
(本小题满分14分)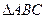 三个顶点坐标为
三个顶点坐标为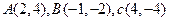 .
.
(Ⅰ)求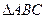 内任一点
内任一点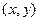 所满足的条件;
所满足的条件;
(Ⅱ)求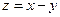 最小值,其中
最小值,其中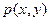 是
是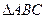 内的整点.
内的整点.
(10分) 22,设数列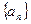 的前n项和为
的前n项和为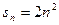 ,
, 为等比数列,
为等比数列,
且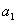 =
=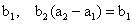
(1)求数列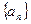 和
和 的通项公式;
的通项公式;
(2)设 ,求数列{
,求数列{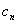 }的前n项和
}的前n项和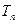
(10分) 如图,货轮在海上以50海里/时的速度沿方位角(从正北方向顺时针转到目标方向线的水平角)为155o的方向航行.为了确定船位,在B点处观测到灯塔A的方位角为125o.半小时后,货轮到达C点处,观测到灯塔A的方位角为80o.求此时货轮与灯塔之间的距离(答案保留最简根号)。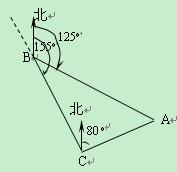
(8分)已知数列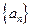 中,
中,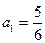 ,以
,以 为系数的二次方程:
为系数的二次方程:
 都有实根
都有实根 ,且满足
,且满足 ①求证:
①求证: 是等比数列;②求
是等比数列;②求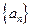 的通项。
的通项。