设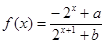 (
( 为实常数).
为实常数).
(1)当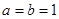 时,证明:
时,证明: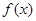 不是奇函数;
不是奇函数;
(2)设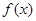 是奇函数,求
是奇函数,求 与
与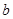 的值;
的值;
(3)在满足(2)且当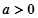 时,若对任意的
时,若对任意的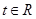 ,不等式
,不等式
恒成立,求 的取值范围.
的取值范围.
椭圆对称轴在坐标轴上,短轴的一个端点与两个焦点构成一个正三角形,焦点到椭圆上的点的最短距离是 ,求这个椭圆方程.
,求这个椭圆方程.
已知方程 ,讨论方程表示的曲线的形状
,讨论方程表示的曲线的形状
如图,已知底角为 的等腰梯形
的等腰梯形 ,底边
,底边 长7 cm,腰长为
长7 cm,腰长为 cm,当一条垂直于底边
cm,当一条垂直于底边 (垂足为
(垂足为 )的直线
)的直线 从左至右移动,(与梯形
从左至右移动,(与梯形 有公共点)时,直线
有公共点)时,直线 把梯形分成两部分,令
把梯形分成两部分,令 ,试写出左边部分的面积
,试写出左边部分的面积 与
与 的函数解析式,并画出大致图象.
的函数解析式,并画出大致图象.
用水清洗一堆蔬菜上残留的农药,对用一定量的水清洗一次的效果作如下假定:用一个单位的水可洗掉蔬菜上残留农药的 ,用水越多洗掉的农药量也越多,但总还有农药残留在蔬菜上.设用
,用水越多洗掉的农药量也越多,但总还有农药残留在蔬菜上.设用 单位量的水清洗一次以后,蔬菜上残留的农药量与本次清洗前残留的农药量之比为函数
单位量的水清洗一次以后,蔬菜上残留的农药量与本次清洗前残留的农药量之比为函数 .
.
⑴试规定 的值,并解释其实际意义;
的值,并解释其实际意义;
⑵试根据假定写出函数 应满足的条件和具有的性质;
应满足的条件和具有的性质;
⑶设 ,现有
,现有 单位量的水,可以清洗一次,也可以把水平均分成两份后清洗两次.试问用那种方案清洗后蔬菜上残留的农药量比较少?说明理由.
单位量的水,可以清洗一次,也可以把水平均分成两份后清洗两次.试问用那种方案清洗后蔬菜上残留的农药量比较少?说明理由.
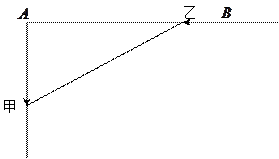
如图甲、乙两船分别沿着箭头方向,从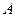 、
、 两地同时开出.已知
两地同时开出.已知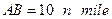 ,甲乙两船的速度分别是16 n mile/h和12 n mile/h,求多少时间后,两船距离最近,最近距离是多少?
,甲乙两船的速度分别是16 n mile/h和12 n mile/h,求多少时间后,两船距离最近,最近距离是多少?
 |