(本小题满分12分)
设椭圆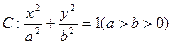 的离心率,
的离心率, 右焦点到直线
右焦点到直线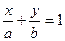 的距离
的距离
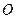 为坐标原点.
为坐标原点.
(Ⅰ)求椭圆 的方程;
的方程;
(II)过点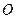 作两条互相垂直的射线,与椭圆
作两条互相垂直的射线,与椭圆 分别交于
分别交于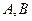 两点,证明:点
两点,证明:点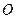 到直线
到直线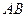 的距离为定值,并求弦
的距离为定值,并求弦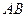 长度的最小值.
长度的最小值.
函数 (A>0,
(A>0, >0)的最小值为-1,其图象相邻两个对称中心之间的距离为
>0)的最小值为-1,其图象相邻两个对称中心之间的距离为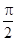 .
.
(1)求函数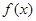 的解析式
的解析式
(2)设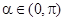 ,则
,则 ,求
,求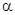 的值.
的值.
已知函数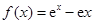 .
.
(Ⅰ)求函数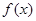 的最小值;
的最小值;
(Ⅱ)求证: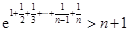
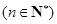 ;
;
(Ⅲ)对于函数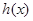 与
与 定义域上的任意实数
定义域上的任意实数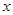 ,若存在常数
,若存在常数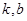 ,使得
,使得 和
和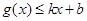 都成立,则称直线
都成立,则称直线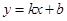 为函数
为函数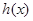 与
与 的“分界线”.设函数
的“分界线”.设函数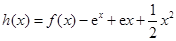 ,
,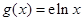 ,
,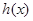 与
与 是否存在“分界线”?若存在,求出
是否存在“分界线”?若存在,求出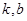 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
设函数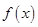 对任意
对任意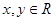 ,都有
,都有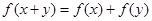 ,当
,当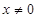 时,
时,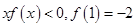
(1)求证: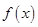 是奇函数;
是奇函数;
(2)试问:在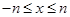 时
时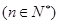 ,
,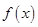 是否有最大值?如果有,求出最大值,如果没有,说明理由.
是否有最大值?如果有,求出最大值,如果没有,说明理由.
(3)解关于x的不等式

(1)求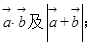
(2) .
.
已知函数 的图象在与
的图象在与 轴交点处的切线方程是
轴交点处的切线方程是 .
.
(I)求函数 的解析式;
的解析式;
(II)设函数 ,若
,若 的极值存在,求实数
的极值存在,求实数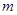 的取值范围以及函数
的取值范围以及函数 取得极值时对应的自变量
取得极值时对应的自变量 的值.
的值.