(本小题满分12分)在调查的 名上网的学生中有
名上网的学生中有 名学生睡眠不好,
名学生睡眠不好, 名不上网的学生中有
名不上网的学生中有 名学生睡眠不好,利用独立性检验的方法来判断是否能以
名学生睡眠不好,利用独立性检验的方法来判断是否能以 的把握认为“上网和睡眠是否有关系”.
的把握认为“上网和睡眠是否有关系”.
附: ;
;
参考数据
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 ,
, .
.
在 中,角
中,角 所对的边分别为
所对的边分别为 ,且
,且 .
.
(1)求角 的值;(2)若
的值;(2)若 为锐角三角形,且
为锐角三角形,且 ,求
,求 的取值范围.
的取值范围.
在等差数列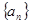 中,
中, ,其前
,其前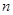 项和为
项和为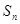 ,等比数列
,等比数列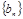 的各项均为正数,
的各项均为正数,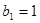 ,公比为
,公比为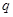 ,且
,且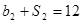 ,
,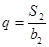 .
.
(1)求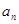 与
与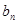 ;(2)设数列
;(2)设数列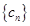 满足
满足 ,求
,求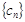 的前
的前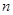 项和
项和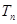 .
.
已知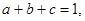
(1)求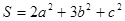 的最小值及取最小值时
的最小值及取最小值时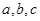 的值。
的值。
(2)若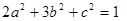 ,求
,求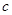 的取值范围。
的取值范围。
已知空间4个球,它们的半径分别为2, 2, 3, 3,每个球都与其他三个球外切,另有一个小球与这4个球都外切,则这个小球的半径为( )
A.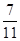 |
B. |
C.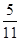 |
D. |
宇宙深处有一颗美丽的行星,这个行星是一个半径为r(r>0)的球。人们在行星表面建立了与地球表面同样的经纬度系统。已知行星表面上的A点落在北纬60°,东经30°;B点落在东经30°的赤道上;C点落在北纬60°,东经90°。在赤道上有点P满足PB两点间的球面距离等于AB两点间的球面距离。
(1)求AC两点间的球面距离;
(2)求P点的经度;
(3)求AP两点间的球面距离。