（本小题满分12分）
某学校为了了解学生的日平均睡眠时间（单位：h），随机选择了n名学生进行调查，下表是这n名学生的日睡眠时间的频率分布表。
| 序号（i） |
分组（睡眠时间） |
频数（人数） |
频率 |
| 1 |
[4,5） |
6 |
0.12 |
| 2 |
[5,6） |
|
0.20 |
| 3 |
[6,7） |
a |
|
| 4 |
[7,8） |
b |
|
| 5 |
[8,9） |
|
0.08 |
（1）求n的值．若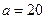
，将表中数据补全，并画出频率分布直方图．
（2）统计方法中，同一组数据常用该组区间的中点值（例如区间
的中点值是5）作为代表．若据此计算的上述数据的平均值为7.2，求
的值，并由此估计该学校学生的日平均睡眠时间在7.5小时以上的概率．
设函数f(x)＝4x3＋ax2＋bx＋5在x＝
与x＝－1时有极值.
(1)写出函数的解析式；
(2)指出函数的单调区间；
(3)求f(x)在[－1，2]上的最大值和最小值．
从参加高一年级迎新数学竞赛的学生中，随机抽取了
名学生的成绩进行统计分析．
(1)完成下列频率分布表，并画出频率分布直方图；
(2)从成绩是[50，60)和[90，100)的学生中选两人，求他们在同一分数段的概率．
| 分 组 |
频数 |
频率 |
 |
2 |
|
 |
10 |
|
 |
20 |
|
 |
15 |
|
 |
3 |
|
| 合计 |
50 |
已知点P在圆x2＋y2＝1上运动，过点P作x轴的垂线，垂足为D，点M在DP的延长线上，且有|DP|＝|MP|.(1)求M点的轨迹方程C；(2)已知直线l过点(0，
)，且斜率为1，求l与C相交所得的弦长．
如图所示，在四棱锥P—ABCD中，底面ABCD是边长为a的正方形，E、F分别为PC、BD的中点，侧面PAD⊥底面ABCD，且PA＝PD＝
AD．
(1)求证：EF∥平面PAD；
(2)求证：平面PAB⊥平面PCD．
已知数列{an}是等差数列，且a3＝5，a2＋a7＝16.
(1)求数列{an}的通项公式；
(2)设bn＝
，求数列{bn}的前
项和Sn．