数列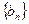
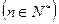 是递增的等比数列,且
是递增的等比数列,且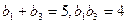 .
.
(1)求数列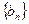 的通项公式;
的通项公式;
(2)若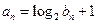 ,求证数列
,求证数列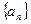 是等差数列;
是等差数列;
(3)设数列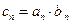 ,求
,求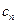 的前n项的和
的前n项的和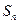
已知P是 内一点,且满足条件
内一点,且满足条件 ,设Q为CP的延长线与AB的交点,令
,设Q为CP的延长线与AB的交点,令 ,用
,用 表示
表示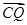 .
.
已知函数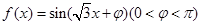 ,
, 为
为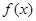 的导函数,若
的导函数,若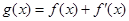 为奇函数,求
为奇函数,求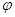 的值.
的值.
已知圆 ,M是圆C上的动点,
,M是圆C上的动点,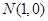 ,MN的垂直平分线交CM于点P,求点P的轨迹方程.
,MN的垂直平分线交CM于点P,求点P的轨迹方程.
已知函数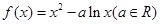
(1)若 ,求函数
,求函数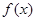 的极值;
的极值;
(2)已知函数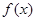 在点
在点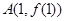 处的切线为
处的切线为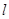 ,若此切线在点A处穿过
,若此切线在点A处穿过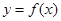 的图像(即函数
的图像(即函数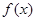 上的动点P在点A附近沿曲线
上的动点P在点A附近沿曲线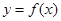 运动,经过点A时从
运动,经过点A时从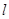 的一侧进入另一侧),求函数
的一侧进入另一侧),求函数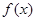 的表达式;
的表达式;
(3)若 ,函数
,函数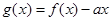 有且仅有一个零点,求实数
有且仅有一个零点,求实数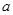 的值.
的值.
已知椭圆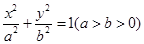 ,F为椭圆的右焦点,点A,B分别为椭圆的上下顶点,过点B作AF的垂线,垂足为M.
,F为椭圆的右焦点,点A,B分别为椭圆的上下顶点,过点B作AF的垂线,垂足为M.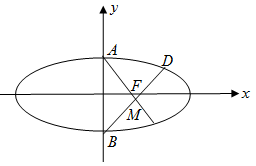
(1)若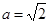 ,
,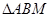 的面积为1,求椭圆方程;
的面积为1,求椭圆方程;
(2)是否存在椭圆,使得点B关于直线AF对称的点D仍在椭圆上,若存在,求椭圆的离心率的值;若不存在,说明理由.