(本小题满分7分)选修4-2:矩阵与变换
设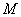 是把坐标平面上的点的横坐标伸长到
是把坐标平面上的点的横坐标伸长到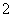 倍,纵坐标伸长到
倍,纵坐标伸长到 倍的伸压变换.
倍的伸压变换.
(Ⅰ)求矩阵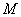 的特征值及相应的特征向量;
的特征值及相应的特征向量;
(Ⅱ)求逆矩阵 以及椭圆
以及椭圆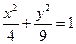 在
在 的作用下的新曲线的方程.
的作用下的新曲线的方程.
(本小题满分13分)设函数 有两个极值点
有两个极值点 ,且
,且 .
.
(1)求实数 的取值范围;
的取值范围;
(2)讨论函数 的单调性;
的单调性;
(3)若对任意的 ,都有
,都有 成立,求实数
成立,求实数 的取值范围.
的取值范围.
(本小题13分)为了保护环境,某工厂在政府部门的鼓励下,进行技术改进:把二氧化碳转化为某种化工产品,经测算,该处理成本 (万元)与处理量
(万元)与处理量 (吨)之间的函数关系可近似的表示为:
(吨)之间的函数关系可近似的表示为: ,且每处理一吨二氧化碳可得价值为20万元的某种化工产品.
,且每处理一吨二氧化碳可得价值为20万元的某种化工产品.
(Ⅰ)当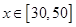 时,判断该技术改进能否获利?如果能获利,求出最大利润;如果不能获利,则国家至少需要补贴多少万元,该工厂才不会亏损?
时,判断该技术改进能否获利?如果能获利,求出最大利润;如果不能获利,则国家至少需要补贴多少万元,该工厂才不会亏损?
(Ⅱ)当处理量为多少吨时,每吨的平均处理成本最少?
(本小题满分13分)直三棱柱 中,
中,
 ,点
,点 在
在 上.
上.
(Ⅰ)若 是
是 中点,求证:
中点,求证: 平面
平面 ;
;
(Ⅱ)当 时,求二面角
时,求二面角 的余弦值.
的余弦值.
(本小题满分12分)已知数列 的前
的前 项和为
项和为 ,且有
,且有 .
.
(1)求数列 的通项公式;
的通项公式;
(2)若 求数列
求数列 的前n项和
的前n项和
设 的内角
的内角 所对的边分别为
所对的边分别为 且
且 .
.
(1)求角 的大小;
的大小;
(2)若 ,求
,求 的周长的取值范围.
的周长的取值范围.