(本小题满分13分)
某鱼塘2009年初有鱼10(万条),每年年终将捕捞当年鱼总量的50%,在第二年年初又将有一部分新鱼放入鱼塘. 根据养鱼的科学技 术知识,该鱼塘中鱼的总量不能超过19.5(万条)(不考虑鱼的自然繁殖和死亡等因素对鱼总量的影响),所以该鱼塘采取对放入鱼塘的新鱼数进行控制,该鱼塘每年只放入新鱼
术知识,该鱼塘中鱼的总量不能超过19.5(万条)(不考虑鱼的自然繁殖和死亡等因素对鱼总量的影响),所以该鱼塘采取对放入鱼塘的新鱼数进行控制,该鱼塘每年只放入新鱼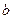 (万条).
(万条).
(I)设第 年年初该鱼塘的鱼总量为
年年初该鱼塘的鱼总量为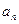 (年初已放入新鱼
(年初已放入新鱼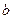 (万条),2010年为第一年),求
(万条),2010年为第一年),求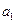 及
及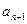 与
与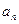 间的关系;
间的关系;
(Ⅱ)当 时,试问能否有效控制鱼塘总量不超过19.5(万条)?若有效,说明理由;若无效,请指出哪一年初开始鱼塘中鱼的总量超过19.5(万条).
时,试问能否有效控制鱼塘总量不超过19.5(万条)?若有效,说明理由;若无效,请指出哪一年初开始鱼塘中鱼的总量超过19.5(万条).