（本小题满分12分）
已知函数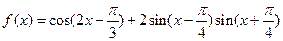
（Ⅰ）求函数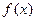
的最小正周期和图象的对称轴方程
（2）求函数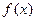在区间
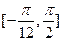上的值域
在平面直角坐标系
中，曲线C1的参数方程为
，
（
为参数)，曲线C2的参数方程为
（
，为参数），在以O为极点，
轴的正半轴为极轴的极坐标系中，射线
与C1，C2各有一个交点．当
时，
这两个交点间的距离为
，当
时，这两个交点重合．
（1）分别说明C1，C2是什么曲线，并求出a与b的值；
（2）设当
时，l与C1，C2的交点分别为A1，B1，当
时，l与C1，C2的交点
分别为A2，B2，求四边形A1A2B2B1的面积．
如图，在圆内画
条线段，将圆分割成两部分；画
条相交线段，彼此分割成
条线段，将圆分割成部分；画
条线段，彼此最多分割成
条线段，将圆最多分割成
部分；画条线段，彼此最多分割成
条线段，将圆最多分割成
部分.
（1）猜想：圆内两两相交的
条线段，彼此最多分割成多少条线段？
（2）记在圆内画条线段，将圆最多分割成
部分，归纳出
与的关系.
（3）猜想数列
的通项公式，根据与的关系及数列的知识，证明你的猜想是否成立.
设命题
:
，其中
，命题
:
，
（1）若
，且
为真，求实数
的取值范围；
（2）若
是
的充分不必要条件，求实数
的取值范围.
已知
，求证：关于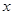
的三个方程
，
，
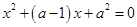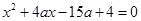中至少有一个方程有实数根.
某企业有两个分厂生产某种零件，按规定内径尺寸（单位：mm）的值落在（29.94，30.06）的零件为优质品。从两个分厂生产的零件中各抽出500件，量其内径尺寸，的结果如下表：
甲厂：
（1）试分别估计两个分厂生产的零件的优质品率；
（2）由于以上统计数据填下面
列联表，并问是否有99%的把握认为“两个分厂生产的零件的质量有差异”。
| 甲 厂 |
乙 厂 |
合计 |
|
| 优质品 |
|||
| 非优质品 |
|||
| 合计 |
附：
，
.