(本小题满分14分)
某厂生产 某种产品的年固定成本为250万元,每生产
某种产品的年固定成本为250万元,每生产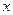 千件,需另投入成本为
千件,需另投入成本为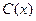 ,当年产量不足
,当年产量不足 80千件时,
80千件时,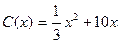 (万元);当年产量不小于80千件时,
(万元);当年产量不小于80千件时,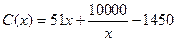 (万元),通过市场分析,若每件售价为500元时,该厂当年生产该产品能全部销售完。
(万元),通过市场分析,若每件售价为500元时,该厂当年生产该产品能全部销售完。
(1)写出年利润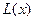 (万元)关于年产量
(万元)关于年产量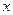 (千件)的函数解析式;
(千件)的函数解析式;
(2)年产量为多少千件时,该厂在这一产品的生产中所获利润最大,最大利润是多少?
(本小题满分14分)
如图,在五面体ABCDEF中,四边形ABCD是平行四边形.
(1)若CF⊥AE,AB⊥AE,求证:平面ABFE⊥平面CDEF;
(2)求证:EF//平面ABCD.
(本小题满分14分)
若定义在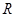 上的函数
上的函数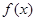 满足
满足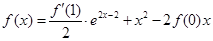 ,
,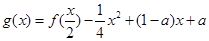 ,
,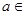
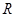 .
.
(Ⅰ)求函数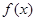 解析式;
解析式;
(Ⅱ)求函数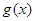 单调区间;
单调区间;
(Ⅲ)若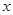 、
、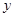 、
、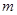 满足
满足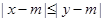 ,则称
,则称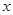 比
比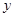 更接近
更接近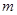 .当
.当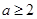 且
且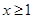 时,试比较
时,试比较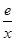 和
和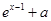 哪个更接近
哪个更接近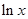 ,并说明理由.
,并说明理由.
(本小题满分13分)
已知椭圆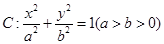 的下顶点为
的下顶点为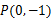 ,
,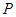 到焦点的距离为
到焦点的距离为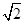 .
.
(Ⅰ)设Q是椭圆上的动点,求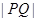 的最大值;
的最大值;
(Ⅱ)若直线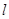 与圆O:
与圆O: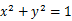 相切,并与椭圆
相切,并与椭圆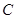 交于不同的两点A、B.当
交于不同的两点A、B.当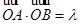 ,且满足
,且满足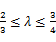 时,求
时,求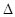 AOB面积S的取值范围.
AOB面积S的取值范围.
(本小题满分12分)
如图,三棱柱 中,
中, 平面
平面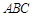 ,
, ,
,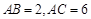 , 点
, 点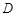 在线段
在线段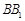 上,且
上,且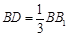 ,
, .
.
(Ⅰ)求证:直线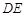 与平面
与平面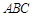 不平行;
不平行;
(Ⅱ)设平面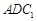 与平面
与平面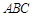 所成的锐二面角为
所成的锐二面角为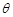 ,若
,若 ,求
,求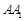 的长;
的长;
(Ⅲ)在(Ⅱ)的条件下,设平面 平面
平面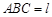 ,求直线
,求直线 与
与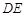 所成的角的余弦值.
所成的角的余弦值.
(本小题满分12分)
某校甲、乙两个班级各有5名编号为1,2,3,4,5的学生进行投篮训练,每人投10次,投中的次数统计如下表:
| 学生 |
1号 |
2号 |
3号 |
4号 |
5号 |
| 甲班 |
6 |
5 |
7 |
9 |
8 |
| 乙班 |
4 |
8 |
9 |
7 |
7 |
(Ⅰ)从统计数据看,甲乙两个班哪个班成绩更稳定(用数据说明)?
(Ⅱ) 若把上表数据作为学生投篮命中率,规定两个班级的1号和2号两名同学分别代表自己的班级参加比赛,每人投篮一次,将甲、乙两个班两名同学投中的次数之和分别记作 和
和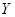 ,试求
,试求 和
和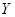 的分布列和数学期望.
的分布列和数学期望.