(本小题满分12分)
已知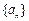 是一个公差大于
是一个公差大于 的等差数列,且满足
的等差数列,且满足 ,
, 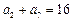 .
.
(1) 求数列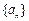 的通项公式;
的通项公式;
(2) 若数列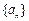 和数列
和数列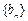 满足等式:
满足等式: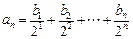 (
( 为正整数), 求数列
为正整数), 求数列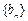 的前
的前 项和
项和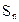 .
.
已知椭圆C的中心在坐标原点,短轴长为4,且有一个焦点与抛物线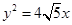 的焦点重合.
的焦点重合.
(Ⅰ)求椭圆C的方程;
(Ⅱ)已知经过定点M(2,0)且斜率不为0的直线 交椭圆C于A、B两点,试问在x轴上是否另存在一个定点P使得
交椭圆C于A、B两点,试问在x轴上是否另存在一个定点P使得 始终平分
始终平分 ?若存在求出
?若存在求出 点坐标;若不存在请说明理由.
点坐标;若不存在请说明理由.
如图,四棱锥S-ABCD中,SD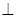 底面ABCD,AB//DC,AD
底面ABCD,AB//DC,AD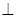 DC,AB=AD=1,DC=SD=2,E为棱SB上任一点.
DC,AB=AD=1,DC=SD=2,E为棱SB上任一点.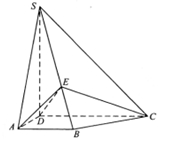
(Ⅰ)求证:无论E点取在何处恒有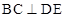 ;
;
(Ⅱ)设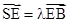 ,当平面EDC
,当平面EDC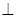 平面SBC时,求
平面SBC时,求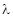 的值;
的值;
(Ⅲ)在(Ⅱ)的条件下求二面角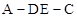 的大小.
的大小.
现有10道题,其中6道甲类题,4道乙类题,张同学从中任取3道题解答.
(I)求张同学至少取到1道乙类题的概率;
(II)已知所取的3道题中有2道甲类题,1道乙类题.设张同学答对甲类题的概率都是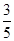 ,答对每道乙类题的概率都是
,答对每道乙类题的概率都是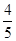 ,且各题答对与否相互独立.用
,且各题答对与否相互独立.用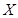 表示张同学答对题的个数,求
表示张同学答对题的个数,求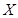 的分布列和数学期望.
的分布列和数学期望.
在 中,角A,B,C所对的边分别为
中,角A,B,C所对的边分别为 .
.
(Ⅰ)叙述并证明正弦定理;
(Ⅱ)设 ,
, ,求
,求 的值.
的值.
已知在等比数列 中,
中,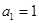 ,且
,且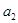 是
是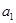 和
和 的等差中项.
的等差中项.
(Ⅰ)求数列 的通项公式;
的通项公式;
(Ⅱ)若数列 满足
满足 ,求
,求 的前
的前 项和
项和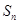 .
.