如图所示,在长方体 中, , ,M是棱 的中点.

(Ⅰ)求异面直线 和 所成的角的正切值;
(Ⅱ)证明:平面 平面
((本小题满分10分)选修4-4:坐标系与参数方程
已知曲线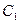 的参数方程为
的参数方程为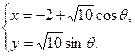
 ,曲线
,曲线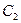 的极坐标方程为
的极坐标方程为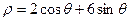
(I)将曲线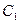 的参数方程化为普通方程,将曲线
的参数方程化为普通方程,将曲线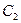 的极坐标方程化为直角坐标方程;
的极坐标方程化为直角坐标方程;
(II)曲线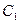 ,
,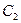 是否相交,若相交,求出公共弦长,若不相交,请说明理由.
是否相交,若相交,求出公共弦长,若不相交,请说明理由.
(本小题满分10分)选修4-1:几何证明选讲
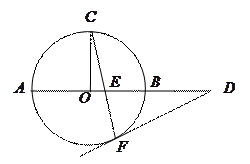
如图,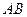 是⊙
是⊙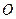 的直径,
的直径,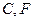 是⊙
是⊙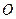 上的两点,
上的两点,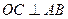 ,过点
,过点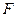 作⊙
作⊙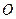 的切线
的切线 交
交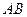 的延长线于点
的延长线于点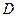 ,连接
,连接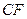 交
交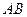 于点
于点 .
. 
求证: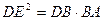
(本小题满分12分)
已知函数: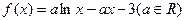
(I) 讨论函数 的单调性;
的单调性;
(II)若函数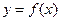 的图象在点
的图象在点 处的切线的倾斜角为
处的切线的倾斜角为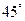 ,对于任意的
,对于任意的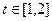 ,若函数
,若函数 在区间
在区间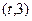 上有最值,求实数
上有最值,求实数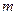 的取值范围;
的取值范围;
(Ⅲ)求证: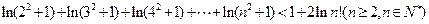 .
.
(本小题满分12分)
已知抛物线C: ,
,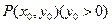 为抛物线上一点,
为抛物线上一点, 为
为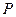 关于
关于 轴对称的点,
轴对称的点, 为坐标原点.
为坐标原点.
(I)若 ,求
,求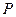 点的坐标;
点的坐标;
(II)若过满足(I)中的点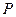 作直线
作直线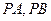 交抛物线
交抛物线 于
于 两点, 且斜率分别为
两点, 且斜率分别为 ,且
,且 ,求证:直线
,求证:直线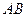 过定点,并求出该定点坐标.
过定点,并求出该定点坐标.
(本小题满分12分)
已知三棱柱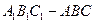 中,三个侧面均为矩形,底面
中,三个侧面均为矩形,底面 为等腰直角三角形,
为等腰直角三角形,  ,点
,点 为棱
为棱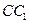 的中点,点
的中点,点 在棱
在棱 上运动.
上运动.
(1)求证

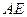 ;
;
(II)当点 运动到某一位置时,恰好使二面角
运动到某一位置时,恰好使二面角 的平面角的余弦值为
的平面角的余弦值为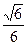 ,求点
,求点 到平面
到平面 的距离;
的距离;
(III)在(II)的条件下,试确定线段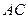 上是否存在一点
上是否存在一点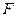 ,使得
,使得 平面
平面 ?若存在,确定其位置;若不存在,说明理由.
?若存在,确定其位置;若不存在,说明理由.