(本小题满分10分)解不等式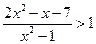
已知函数f(x)=(x2+bx+c)ex,其中b,c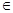 R为常数.
R为常数.
(Ⅰ)若b2>4(c-1),讨论函数f(x)的单调性;
(Ⅱ)若b2≤4(c-1),且
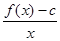 =4,试证:-6≤b≤2.
=4,试证:-6≤b≤2.
设数列 的前n项和为
的前n项和为 ,点
,点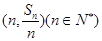 均在函数y=3x-2的图像上。
均在函数y=3x-2的图像上。
(Ⅰ)求数列 的通项公式;
的通项公式;
(Ⅱ)设 ,
, 是数列
是数列 的前n项和,求使得
的前n项和,求使得 对所有
对所有 都成立的最小正整数m。
都成立的最小正整数m。
如图,在四棱锥P-ABCD中,底面为直角梯形,AD∥BC,∠BAD=90°,PA⊥底面ABCD,且PA=AD=AB=2BC,M、N分别为PC、PB的中点.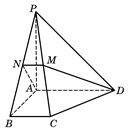
(Ⅰ)求证:PB⊥DM;
(Ⅱ)求CD与平面ADMN所成的角
袋中装着标有数学1,2,3,4,5的小球各2个,从袋中任取3个小球,按3个小球上最大数字的9倍计分,每个小球被取出的可能性都相等,用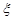 表示取出的3个小球上的最大数字,求:
表示取出的3个小球上的最大数字,求:
(1)取出的3个小球上的数字互不相同的概率;
(2)随机变量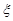 的概率分布和数学期望;
的概率分布和数学期望;
(3)计分介于20分到40分之间的概率.
已知函数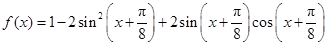 .求:
.求:
(I)函数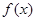 的最小正周期;
的最小正周期;
(II)函数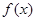 的单调增区间.
的单调增区间.