已知A(-2,0),B(2,0),动点P与A、B两点连线的斜率分别为 和
和 ,且满足
,且满足 ·
· ="t" (t≠0且t≠-1).
="t" (t≠0且t≠-1).
(1)求动点P的轨迹C的方程;
(2)当t<0时,曲线C的两焦点为F1,F2,若曲线C上存在点Q使得∠F1QF2=120O,
求t的取值范围.
已知椭圆 (a>b>0)的离心率为
(a>b>0)的离心率为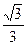 ,过右焦点F的直线
,过右焦点F的直线 与椭圆C相交于AB两点,当
与椭圆C相交于AB两点,当 斜率为1时,坐标原点O到
斜率为1时,坐标原点O到 的距离为
的距离为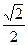
(Ⅰ)求a,b的值;
(Ⅱ)C上是否存在点P,使得当l绕F转到某一位置时,有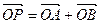 成立?
成立?
若存在,求出所有的P的坐标与l的方程;若不存在,说明理由。
若数列 的前
的前 项和
项和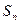 是
是 二项展开式中各项系数的和
二项展开式中各项系数的和 .
.
(Ⅰ)求 的通项公式;
的通项公式;
(Ⅱ)若数列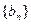 满足
满足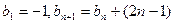 ,且
,且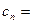
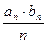 ,求数列
,求数列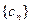 的通项及其前
的通项及其前 项和
项和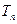 。
。
已知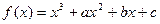 的图像与y轴交于点(0,2),
的图像与y轴交于点(0,2),
并且在x=1处切线的方向向量为 。
。
(1)若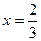 是函数
是函数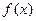 的极值点,求
的极值点,求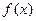 的解析式;
的解析式;
(2)若函数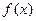 在区间[
在区间[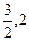 ]单调递增,求实数b的取值范围。
]单调递增,求实数b的取值范围。
如图,四棱锥P-ABCD中,底面ABCD为矩形,
PA 底面ABCD,PA=AB=
底面ABCD,PA=AB=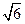 ,点E是棱PB的中点。
,点E是棱PB的中点。
(1)AD与平面PBC的距离;
(2)若AD= ,求二面角A-EC-D的平面角的余弦值。
,求二面角A-EC-D的平面角的余弦值。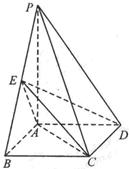
(选修4—5:不等式选讲)设函数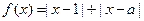
(1)若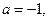 解不等式
解不等式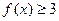 ;(2)如果
;(2)如果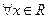 ,
, ,求
,求 的取值范围。
的取值范围。