设函数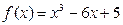 ,
, 。
。
(1)求函数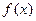 的单调区间和极值。
的单调区间和极值。
(2)若关于 的方程
的方程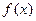 ="a" 有三个不同实根,求实数a的取值范围。
="a" 有三个不同实根,求实数a的取值范围。
(3)已知当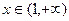 时,
时, 恒成立,求实数
恒成立,求实数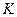 的取值范围。
的取值范围。
已知 , 计算:
, 计算:
(1)  (2)
(2) 
求值:(1) ; (2)
; (2)
(本小题满分12分)
某矩形花园 ,
,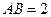 ,
,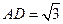 ,
, 是
是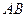 的中点,在该花园中有一花圃其形状是以
的中点,在该花园中有一花圃其形状是以 为直角顶点的内接Rt△
为直角顶点的内接Rt△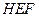 ,其中E、F分别落在线段
,其中E、F分别落在线段 和线段
和线段 上如图.分别记
上如图.分别记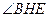 为
为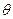 (
( ),
),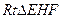 的周长为
的周长为 ,
,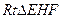 的面积为
的面积为
(1)试求 的取值范围;
的取值范围;
(2)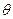 为何值时
为何值时 的值为最小;并求
的值为最小;并求 的最小值.
的最小值.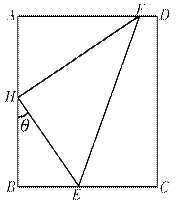
(本小题满分14分)
已知点A、B、C的坐标分别为A(3,0)、B(0,3)、C(cosα,sinα),α∈(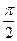 ,
,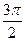 ).
).
(1)若|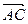 |=|
|=|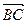 |,求角α的值;
|,求角α的值;
(2)若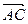 ·
·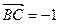 ,求
,求 的值.
的值.
(本小题满分12分)
已知函数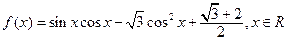 。
。
(1)求函数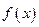 的最小正周期及函数取最小值时自变量
的最小正周期及函数取最小值时自变量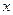 的集合;
的集合;
(2)确定函数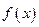 的单调递增区间;
的单调递增区间;
(3)若函数y=sin2x的图象向右平移m个单位(|m|<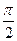 ),向上平移n个单位后得到函数y=f(x)的图象,求实数m、n的值。
),向上平移n个单位后得到函数y=f(x)的图象,求实数m、n的值。