已知数列 的前n项和为
的前n项和为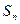 ,且满足
,且满足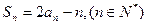
(Ⅰ)求 的值;
的值;
(Ⅱ)证明 是等比数列,并求
是等比数列,并求 ;
;
(Ⅲ)若 ,数列
,数列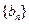 的前n项和为
的前n项和为 。
。
(本小题满分13分)已知集合A=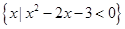 ,B=
,B=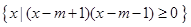 ,
,
(Ⅰ)当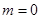 时,求
时,求 .
.
(Ⅱ)若 :
: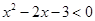 ,
, :
: ,且
,且 是
是 的必要不充分条件,求实数
的必要不充分条件,求实数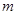 的取值范围。
的取值范围。
(本小题满分13分)实数 满足圆的标准方程
满足圆的标准方程 ,
,
(Ⅰ)求 的最小值;
的最小值;
(Ⅱ)求定点 到圆上点的最大值.
到圆上点的最大值.
设函数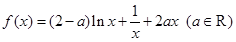 .
.
(1)当 时,求
时,求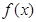 的极值;
的极值;
(2)当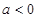 时,求
时,求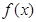 的单调区间;
的单调区间;
(3)若对任意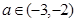 及
及 ,恒有
,恒有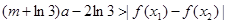 成立,求
成立,求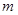 的取值范围
的取值范围
已知等差数列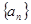 的公差大于0,且
的公差大于0,且 是方程
是方程 的两根,数列
的两根,数列 的前
的前 项的和为
项的和为 ,且
,且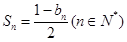 .
.
(1)求数列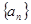 ,
, 的通项公式;
的通项公式;
(2)记 ,求证:
,求证: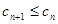 ;
;
(3)求数列 的前
的前 项和
项和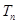 .
.
过点Q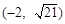 作圆C:
作圆C: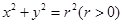 的切线,切点为D,且QD=4.
的切线,切点为D,且QD=4.
(1)求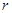 的值;
的值;
(2)设P是圆C上位于第一象限内的任意一点,过点P作圆C的切线l,且l交x轴于点A,交y轴于点B,设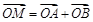 ,求
,求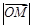 的最小值(O为坐标原点).
的最小值(O为坐标原点).