将A、B两枚骰子各抛掷一次,观察向上的点数,问:
(I)共有多少种不同的结果?
(II)两枚骰子点数之和是3的倍数的结果有多少种?
(III)两枚骰子点数之和是3的倍数的概率是多少?
(本小题 满分12分)已知 是定义在
是定义在 上的偶函数,且
上的偶函数,且 时,
时, .
.
(1)求 ,
, ;
;
(2)求函数 的表达式;
的表达式;
(3)若 ,求
,求 的取值范围.
的取值范围.
(本小题满分12分)已知命题p: 命题q:1-m≤x≤1+m,m>0,
命题q:1-m≤x≤1+m,m>0,
若¬p是¬q的必要不充分条件,求实数m的取值范围.
(本小题满分10分)已知函数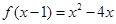 ,求函数
,求函数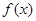 ,
,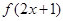 的解析式.
的解析式.
(本大题13分)已知函数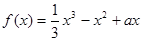 (
(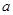 为常数)
为常数)
(1)若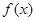 在区间
在区间 上单调递减,求
上单调递减,求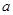 的取值范围;
的取值范围;
(2)若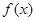 与直线
与直线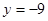 相切:
相切:
(ⅰ)求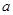 的值;
的值;
(ⅱ)设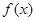 在
在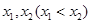 处取得极值,记点M (
处取得极值,记点M ( ,
,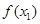 ),N(
),N(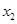 ,
,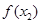 ),P(
),P(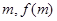 ),
),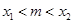 , 若对任意的m
, 若对任意的m 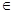 (
( , x
, x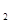 ),线段MP与曲线f(x)均有异于M,P的公共点,试确定
),线段MP与曲线f(x)均有异于M,P的公共点,试确定 的最小值,并证明你的结论.
的最小值,并证明你的结论.
(本大题9分)已知大于1的正数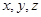 满足
满足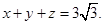
(1)求证: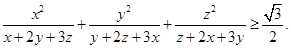
(2)求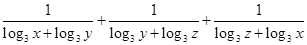 的最小值.
的最小值.