(本小题满分14分)
等差数列 的各项均为正数,
的各项均为正数,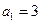 ,前
,前 项和为
项和为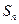
 ,
,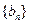 为等比数列,
为等比数列, 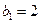 ,且
,且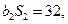
 .
.
(1)求 与
与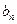 ;
;
(2)求数列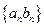 的前
的前 项和
项和 。
。
(3)若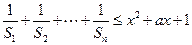 对任意正整数
对任意正整数 和任意
和任意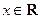 恒成立,求实数
恒成立,求实数 的取值范围.
的取值范围.
(本小题满分12分)已知条件 (a>0)和条件
(a>0)和条件 ,
,
请选取适当的实数 的值,分别利用所给的两个条件作为A、B构造命题:“若A则B”,并使得构造的原命题为真命题,而其逆命题为假命题.则这样的一个原命题可以是什么?并说明为什么这一命题是符合要求的命题.
的值,分别利用所给的两个条件作为A、B构造命题:“若A则B”,并使得构造的原命题为真命题,而其逆命题为假命题.则这样的一个原命题可以是什么?并说明为什么这一命题是符合要求的命题.
(本小题满分14分)对于函数 ,若存在
,若存在 ,使
,使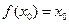 成立,则称
成立,则称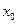 为
为 的不动点。如果函数
的不动点。如果函数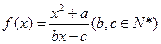 有且仅有两个不动点
有且仅有两个不动点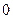 、
、 ,且
,且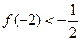 。
。
(1)试求函数 的单调区间;
的单调区间;
(2)已知各项均为负的数列 满足
满足 ,求证:
,求证: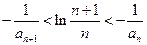 ;
;
(3)设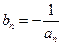 ,
,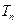 为数列
为数列 的前
的前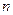 项和,求证:
项和,求证: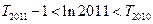 。
。
(本小题满分13分)
已知二次函数 ,直线
,直线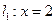 ,直线
,直线
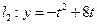 (其中
(其中 ,
,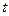 为常数);.若直线
为常数);.若直线 1、
1、 2与函数
2与函数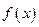 的图象以及
的图象以及 、
、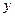 轴与函数
轴与函数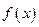 的图象所围成的封闭图形如图阴影所示.
的图象所围成的封闭图形如图阴影所示.
(Ⅰ)求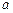 、
、 、
、 的值;
的值;
(Ⅱ)求阴影面积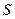 关于
关于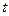 的函数
的函数 的解析式;
的解析式;
(Ⅲ)若 问是否存在实数
问是否存在实数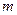 ,使得
,使得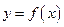 的图象与
的图象与 的图象有且只有两个不同的交点?若存在,求出
的图象有且只有两个不同的交点?若存在,求出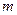 的值;若不存在,说明理由.
的值;若不存在,说明理由.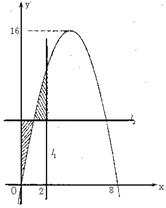
(本小题满分12分)已知△ABC的面积S满足 , 且
, 且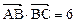 ,
,  与
与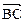 的夹角为
的夹角为 .
.
(I) 求 的取值范围;
的取值范围;
(II)求函数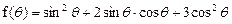 的最小值.
的最小值.
(本小题满分12分)已知函数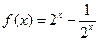 .
.
(1)若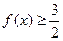 ,求x的取值范围;
,求x的取值范围;
(2)若 对于
对于 ∈[1,2]恒成立,求实数m的取值范围.
∈[1,2]恒成立,求实数m的取值范围.