(本小题满分14分)为研究我校高二年级的男生身高,随机抽取40名男生,实测身高数据(单位:厘米)如下:
171 173 163 169 166 167 168.5 160 170 165
175 169 167 156 165.5 168 170 184 168 174
165 170 174 161 177 175.5 173 164 175 171.5
176 159 172 181 175.5 165 163 173 170.5 171
(I)依据题目提示作出频率分布表;
(Ⅱ)在(I)的条件下画出频率分布直方图并且画出其频率分布折线图;
(Ⅲ)试利用频率分布的直方图估计样本的平均数。
【解】(I)最低身高156cm,最高身高184cm,确定组距为4,作频率分布表如下:
| 身高(cm) |
频数累计 |
频数 |
频率(%) |
 |
|
|
|
| |
|
|
|
| |
|
|
|
| |
|
|
|
| |
|
|
|
| |
|
|
|
 |
|
|
|
(Ⅱ)频率直方图如下:
已知等差数列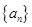 的前n项和为
的前n项和为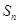 ,满足
,满足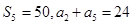 ,
,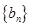 为递增的等比数列,且
为递增的等比数列,且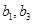 是方程
是方程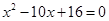 的两个根.
的两个根.
(I)求数列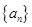 ,
,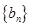 的通项公式;
的通项公式;
(II)若数列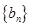 满足
满足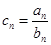 ,求数列
,求数列 的前n项和
的前n项和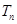 .
.
如图,在三棱柱 中,四边形
中,四边形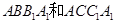 都为矩形.
都为矩形.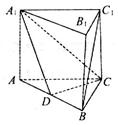
(I)设D是AB的中点,证明:直线 平面
平面 ;
;
(II)在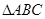 中,若
中,若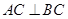 ,证明:直线
,证明:直线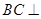 平面
平面 .
.
已知函数 .
.
(I)求函数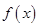 的最小正周期;
的最小正周期;
(II)将函数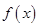 的图象向左平移
的图象向左平移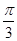 个单位,得到函数
个单位,得到函数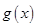 的图象.在
的图象.在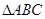 中,角A,B,C的对边分别为
中,角A,B,C的对边分别为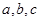 ,若
,若 ,求
,求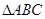 的面积.
的面积.
某省为了研究雾霾天气的治理,一课题组对省内24个城市进行了空气质量的调查,按地域特点把这些城市分成了甲、乙、丙三组.已知三组城市的个数分别为4,8,12,课题组用分层抽样的方法从中抽取6个城市进行空气质量的调查.
(I)求每组中抽取的城市的个数;
(II)从已抽取的6个城市中任抽两个城市,求两个城市不来自同一组的概率.
(本小题满分14分)已知关于x的函数 .
.
(I)求函数 在点
在点 处的切线方程;
处的切线方程;
(II)求函数 有极小值,试求a的取值范围;
有极小值,试求a的取值范围;
(III)若在区间 上,函数
上,函数 不出现在直线
不出现在直线 的上方,试求a的最大值.
的上方,试求a的最大值.