已知函数 .
.
(I)求函数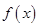 的最小正周期;
的最小正周期;
(II)将函数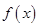 的图象向左平移
的图象向左平移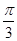 个单位,得到函数
个单位,得到函数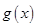 的图象.在
的图象.在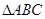 中,角A,B,C的对边分别为
中,角A,B,C的对边分别为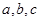 ,若
,若 ,求
,求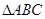 的面积.
的面积.
某人在一山坡P处观看对面山顶上的一座铁塔,如图所示,塔高BC=80(米),塔所在的山高OB=220(米),OA=200(米),图中所示的山坡可视为直线l,且点P在直线l上,l与水平地面的夹角为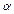 ,tan
,tan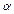 =
= .试问,此人距水平地面多高时,观看塔的视角∠BPC最大(不计此人的身高)?
.试问,此人距水平地面多高时,观看塔的视角∠BPC最大(不计此人的身高)?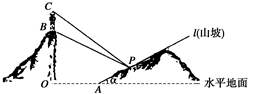
已知直线l与两坐标轴围成的三角形的面积为3,分别求满足下列条件的直线l的方程:
(1)过定点A(-3,4);(2)斜率为 .
.
已知两点A(-1,2),B(m,3).
(1)求直线AB的方程;
(2)已知实数m∈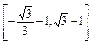 ,求直线AB的倾斜角
,求直线AB的倾斜角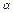 的取值范围.
的取值范围.
已知线段PQ两端点的坐标分别为(-1,1)、(2,2),若直线l:x+my+m=0与线段PQ有交点,求m的取值范围.
(1)求 的导数;
的导数;
(2)求 的导数;
的导数;
(3)求 的导数;
的导数;
(4)求y= 的导数;
的导数;
(5)求y= 的导数。
的导数。